Advertisements
Advertisements
प्रश्न
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
उत्तर
The distance d between two points `(x_1,y_1)` and `(x_2,y_2)`
`d = sqrt((x_1- x_2)^2 + (y_1 - y_2)^2)`
In a square, all the sides are of equal length. The diagonals are also equal to each other. Also in a square, the diagonal is equal to `sqrt2` times the side of the square.
Here let the two points which are said to be the opposite vertices of a diagonal of a square be A(−1,2) and C(3,2).
Let us find the distance between them which is the length of the diagonal of the square.
`AC = sqrt((-1-3)^2 + (2 - 2)^2 )`
`= sqrt((-4)^2 +(0)^2)`
`= sqrt(16)`
AC = 4
Now we know that in a square,
The side of the square = `"Diagonal of the square"/sqrt2`
The side of the square = `2sqrt2`
Now, a vertex of a square has to be at equal distances from each of its adjacent vertices.
Let P(x, y) represent another vertex of the same square adjacent to both ‘A’ and ‘C’
`AP = sqrt((-1-x)^2 + (2 -y)^2)`
`CP = sqrt((3 - x)^2 + (2 - x)^2)`
But these two are nothing but the sides of the square and need to be equal to each other.
AP = CP
`sqrt((-1-x)^2 + (2 - y)^2) = sqrt((3 - x)^2 + (2 - y)^2)`
Squaring on both sides we have,
`AP = sqrt((-1-x)^2 + (2 - y)^2)`
`2sqrt(2) = sqrt((-1-1)^2 + (2 - y)^2)`
`2sqrt2 = sqrt((-2)^2 + (2 - y)^2)`
Squaring on both sides,
`8 = (-2)^2 + (2 - y)^2`
`8 = 4 + 4 = y^2 - 4y`
`0 = y^2 - 4y`
We have a quadratic equation. Solving for the roots of the equation we have,
`y^2 - 4y = 0`
y(y - 4) = 0
The roots of this equation are 0 and 4.
Therefore the other two vertices of the square are (1, 0) and (1,4)
APPEARS IN
संबंधित प्रश्न
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
If the distances of P(x, y) from A(5, 1) and B(–1, 5) are equal, then prove that 3x = 2y
Find the value of a when the distance between the points (3, a) and (4, 1) is `sqrt10`
Find the distance of a point (7 , 5) from another point on the x - axis whose abscissa is -5.
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
Prove that the points (1 ,1),(-4 , 4) and (4 , 6) are the certices of an isosceles triangle.
Prove that the points (7 , 10) , (-2 , 5) and (3 , -4) are vertices of an isosceles right angled triangle.
ABC is an equilateral triangle . If the coordinates of A and B are (1 , 1) and (- 1 , -1) , find the coordinates of C.
A(2, 5), B(-2, 4) and C(-2, 6) are the vertices of a triangle ABC. Prove that ABC is an isosceles triangle.
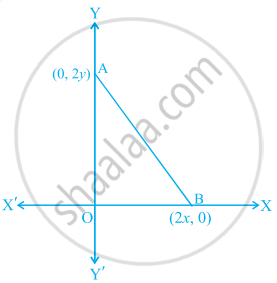
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.