Advertisements
Advertisements
प्रश्न
Prove that the points (1 ,1),(-4 , 4) and (4 , 6) are the certices of an isosceles triangle.
उत्तर
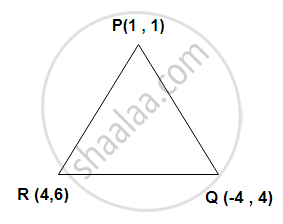
PQ = `sqrt ((1 + 4)^2 + (1 - 4)^2) = sqrt (25 + 9) = sqrt 34` units
QR = `sqrt ((-4-4)^2 + (4 - 6)^2) = sqrt (64 + 4) sqrt 68` units
PR = `sqrt ((4 - 1)^2 + (6 - 1)^2) = sqrt (9 + 25) = sqrt 34` units
∵ PQ = QR
∴ P,Q and R are the vertices of an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
Find the distance between the points
A(1,-3) and B(4,-6)
Find the distance of the following points from the origin:
(ii) B(-5,5)
If the point A(x,2) is equidistant form the points B(8,-2) and C(2,-2) , find the value of x. Also, find the value of x . Also, find the length of AB.
Show that the ▢PQRS formed by P(2, 1), Q(–1, 3), R(–5, –3) and S(–2, –5) is a rectangle.
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
Find the distance between the origin and the point:
(8, -15)
Find the point on y-axis whose distances from the points A (6, 7) and B (4, -3) are in the ratio 1: 2.
By using the distance formula prove that each of the following sets of points are the vertices of a right angled triangle.
(i) (6, 2), (3, -1) and (- 2, 4)
(ii) (-2, 2), (8, -2) and (-4, -3).
Find distance CD where C(– 3a, a), D(a, – 2a)
