Advertisements
Advertisements
प्रश्न
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
उत्तर
Let the point on x-axis be P (x,0)
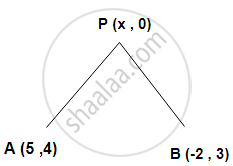
Given ,
PA = PB
PA2 = PB2
(x - 5)2 + (0 - 4)2 = (x + 2)2 + (0 - 3)2
x2 + 25 - 10x + 16 = x2 + 4 + 4x + 9
⇒ - 14 x + 28 = 0
⇒ 14 x = 28
⇒ x = 2
∴ The point on x-axis is (2 , 0)
APPEARS IN
संबंधित प्रश्न
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
Find the distance between the following pairs of points:
(2, 3), (4, 1)
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Find the distance between the following pair of points.
L(5, –8), M(–7, –3)
Show that the ▢PQRS formed by P(2, 1), Q(–1, 3), R(–5, –3) and S(–2, –5) is a rectangle.
Prove taht the points (-2 , 1) , (-1 , 4) and (0 , 3) are the vertices of a right - angled triangle.
Show that the points (2, 0), (– 2, 0) and (0, 2) are vertices of a triangle. State the type of triangle with reason
AOBC is a rectangle whose three vertices are A(0, 3), O(0, 0) and B(5, 0). The length of its diagonal is ______.
The point which divides the lines segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
The point P(–2, 4) lies on a circle of radius 6 and centre C(3, 5).
