Advertisements
Advertisements
Question
Find the point on the x-axis equidistant from the points (5,4) and (-2,3).
Solution
Let the point on x-axis be P (x,0)
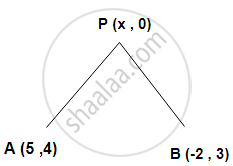
Given ,
PA = PB
PA2 = PB2
(x - 5)2 + (0 - 4)2 = (x + 2)2 + (0 - 3)2
x2 + 25 - 10x + 16 = x2 + 4 + 4x + 9
⇒ - 14 x + 28 = 0
⇒ 14 x = 28
⇒ x = 2
∴ The point on x-axis is (2 , 0)
APPEARS IN
RELATED QUESTIONS
Find the distance of a point P(x, y) from the origin.
Two opposite vertices of a square are (-1, 2) and (3, 2). Find the coordinates of other two
vertices.
Find the distance between the points
A(1,-3) and B(4,-6)
Determine whether the points are collinear.
L(–2, 3), M(1, –3), N(5, 4)
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
PQR is an isosceles triangle . If two of its vertices are P (2 , 0) and Q (2 , 5) , find the coordinates of R if the length of each of the two equal sides is 3.
Show that the points (2, 0), (–2, 0), and (0, 2) are the vertices of a triangle. Also, a state with the reason for the type of triangle.
Calculate the distance between the points P (2, 2) and Q (5, 4) correct to three significant figures.
If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x
The distance of the point P(–6, 8) from the origin is ______.
