Advertisements
Advertisements
Question
If the distance between point L(x, 7) and point M(1, 15) is 10, then find the value of x
Solution
Let L(x1, y1) = L(x, 7) and M (x2, y2) = M(1, 15)
x1 = x, y1 = 7, x2 = 1, y2 = 15
By distance formula,
d(L, M) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(L, M) = `sqrt((1 - x)^2 + (15 - 7)^2`
∴ 10 = `sqrt((1 - x)^2 + 8^2`
∴ 100 = (1 – x)2 + 64 ......[Squaring both sides]
∴ (1 – x)2 = 100 – 64
∴ (1 – x)2 = 36
∴ 1 – x = `+- sqrt(36)` .....[Taking square root of both sides]
∴ 1 – x = ± 6
∴ 1 – x = 6 or 1 – x = – 6
∴ x = – 5 or x = 7
∴ The value of x is – 5 or 7.
APPEARS IN
RELATED QUESTIONS
If A(4, 3), B(-1, y) and C(3, 4) are the vertices of a right triangle ABC, right-angled at A, then find the value of y.
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
If the point P(2, 2) is equidistant from the points A(−2, k) and B(−2k, −3), find k. Also find the length of AP.
Find the values of x, y if the distances of the point (x, y) from (-3, 0) as well as from (3, 0) are 4.
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3)
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Find the distance of the following points from the origin:
(iii) C (-4,-6)
For what values of k are the points (8, 1), (3, –2k) and (k, –5) collinear ?
Find the distances between the following point.
A(a, 0), B(0, a)
Find the distances between the following point.
P(–6, –3), Q(–1, 9)
Find the distance of the following point from the origin :
(5 , 12)
Find the distance of the following point from the origin :
(8 , 15)
Find the value of m if the distance between the points (m , -4) and (3 , 2) is 3`sqrt 5` units.
Prove that the following set of point is collinear :
(5 , 5),(3 , 4),(-7 , -1)
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
Find the distance between the following pairs of points:
`(3/5,2) and (-(1)/(5),1(2)/(5))`
Find the distance between the origin and the point:
(-8, 6)
Find a point on the y-axis which is equidistant from the points (5, 2) and (-4, 3).
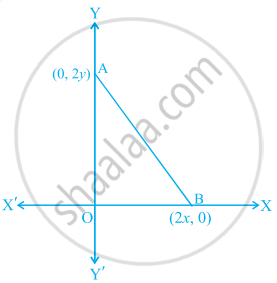
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.