Advertisements
Advertisements
Question
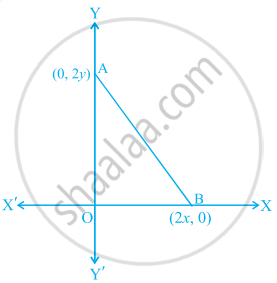
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Options
(x, y)
(y, x)
`(x/2, y/2)`
`(y/2, x/2)`
Advertisements
Solution
The coordinates of the point which is equidistant from the three vertices of the ∆AOB as shown in the figure is (x, y).
Explanation:
Let the coordinate of the point which is equidistant from the three vertices 0(0, 0), A(0, 2y) and B(2x, 0) is P(h, k).
Then, PO = PA = PB
⇒ (PO)2 = (PA)2 = (PB)2 ...(i)
By distance formula,
`[sqrt((h - 0)^2 + (k - 0)^2)]^2`
= `[sqrt((h - 0)^2 + (k - 2y)^2)]^2`
= `[sqrt((h - 2x)^2 + (k - 0)^2)]^2`
⇒ h2 + k2 = h2 + (k – 2y)2
= (h – 2x)2 + k2 ...(ii)
Taking first two equations, we get
h2 + k2 = h2 + (k – 2y)2
⇒ k2 = k2 + 4y2 – 4yk
⇒ 4y(y – k) = 0
⇒ y = k ...[∵ y ≠ 0]
Taking first and third equations, we get
h2 + k2 = (h – 2x)2 + k2
⇒ h2 = h2 + 4x2 – 4xh
⇒ 4x(x – h) = 0
⇒ x = h ...[∵ x ≠ 0]
∴ Required points = (h, k) = (x, y)
APPEARS IN
RELATED QUESTIONS
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
Check whether (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
Find the distance between the points:
P(a + b, a - b) and Q(a - b, a + b)
For what values of k are the points (8, 1), (3, –2k) and (k, –5) collinear ?
Show that the ▢PQRS formed by P(2, 1), Q(–1, 3), R(–5, –3) and S(–2, –5) is a rectangle.
Find the distance between the following point :
(p+q,p-q) and (p-q, p-q)
Find the distance between the following point :
(sin θ , cos θ) and (cos θ , - sin θ)
P(5 , -8) , Q (2 , -9) and R(2 , 1) are the vertices of a triangle. Find tyhe circumcentre and the circumradius of the triangle.
Prove that the points (6 , -1) , (5 , 8) and (1 , 3) are the vertices of an isosceles triangle.
Prove that the points (0 , -4) , (6 , 2) , (3 , 5) and (-3 , -1) are the vertices of a rectangle.
Find the coordinates of the points on the y-axis, which are at a distance of 10 units from the point (-8, 4).
Show that the points P (0, 5), Q (5, 10) and R (6, 3) are the vertices of an isosceles triangle.
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
The point which divides the lines segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
The distance between the point P(1, 4) and Q(4, 0) is ______.
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
The coordinates of the centroid of ΔEHJ are ______.
The distance between the points (0, 5) and (–3, 1) is ______.
Show that Alia's house, Shagun's house and library for an isosceles right triangle.
