Advertisements
Advertisements
Question
Ayush starts walking from his house to office. Instead of going to the office directly, he goes to a bank first, from there to his daughter’s school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office? (Assume that all distances covered are in straight lines). If the house is situated at (2, 4), bank at (5, 8), school at (13, 14) and office at (13, 26) and coordinates are in km.
Advertisements
Solution
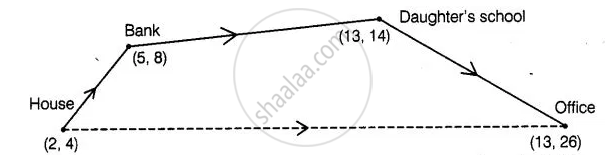
By given condition, we drawn a figure in which every place are indicated with his coordinates and direction also.
We know that,
Distance between two points (x1, y1) and (x2, y2),
d = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
Now, distance between house and bank
= `sqrt((5 - 2)^2 + (8 - 4)^2`
= `sqrt((3)^2 + (4)^2`
= `sqrt(9 + 16)`
= `sqrt(25)`
= 5
Distance between bank and daughter's school
= `sqrt((13 - 5)^2 + (14 - 8)^2`
= `sqrt((8)^2 + (6)^2`
= `sqrt(64 + 36)`
= `sqrt(100)`
= 10
Distance between daughter's school and office
= `sqrt((13 - 13)^2 + (26 - 14)^2`
= `sqrt(0 + (12)^2`
= 12
Total distance (House + Bank + School + Office) travelled
= 5 + 10 + 12
= 27 units
Distance between house to offices
= `sqrt((13 - 2)^2 + (26 - 4)^2`
= `sqrt((11)^2 + (22)^2`
= `sqrt(121 + 484)`
= `sqrt(605)`
= 24.59
= 24.6 km
So, extra distance travelled by Ayush in reaching his office = 27 – 24.6 = 2.4 km.
Hence, the required extra distance travelled by Ayush is 2.4 km.
APPEARS IN
RELATED QUESTIONS
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
Find the value of x, if the distance between the points (x, – 1) and (3, 2) is 5.
Find the coordinates of the circumcentre of the triangle whose vertices are (8, 6), (8, – 2) and (2, – 2). Also, find its circum radius
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
An equilateral triangle has two vertices at the points (3, 4) and (−2, 3), find the coordinates of the third vertex.
Find the co-ordinates of points of trisection of the line segment joining the point (6, –9) and the origin.
Show that the points A(1, 2), B(1, 6), C(1 + 2`sqrt3`, 4) are vertices of an equilateral triangle.
Find the distance between the following pairs of point in the coordinate plane :
(7 , -7) and (2 , 5)
Find the distance of a point (12 , 5) from another point on the line x = 0 whose ordinate is 9.
Prove that the following set of point is collinear :
(5 , 1),(3 , 2),(1 , 3)
Prove that the points (0 , 2) , (1 , 1) , (4 , 4) and (3 , 5) are the vertices of a rectangle.
Show that the points (2, 0), (–2, 0), and (0, 2) are the vertices of a triangle. Also, a state with the reason for the type of triangle.
Points A (-3, -2), B (-6, a), C (-3, -4) and D (0, -1) are the vertices of quadrilateral ABCD; find a if 'a' is negative and AB = CD.
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
A circle drawn with origin as the centre passes through `(13/2, 0)`. The point which does not lie in the interior of the circle is ______.
The distance between the point P(1, 4) and Q(4, 0) is ______.
A circle has its centre at the origin and a point P(5, 0) lies on it. The point Q(6, 8) lies outside the circle.
Find the points on the x-axis which are at a distance of `2sqrt(5)` from the point (7, – 4). How many such points are there?
Read the following passage:
|
Use of mobile screen for long hours makes your eye sight weak and give you headaches. Children who are addicted to play "PUBG" can get easily stressed out. To raise social awareness about ill effects of playing PUBG, a school decided to start 'BAN PUBG' campaign, in which students are asked to prepare campaign board in the shape of a rectangle: One such campaign board made by class X student of the school is shown in the figure.
|
Based on the above information, answer the following questions:
- Find the coordinates of the point of intersection of diagonals AC and BD.
- Find the length of the diagonal AC.
-
- Find the area of the campaign Board ABCD.
OR - Find the ratio of the length of side AB to the length of the diagonal AC.
- Find the area of the campaign Board ABCD.
