Advertisements
Advertisements
प्रश्न
Prove that the points (6 , -1) , (5 , 8) and (1 , 3) are the vertices of an isosceles triangle.
उत्तर
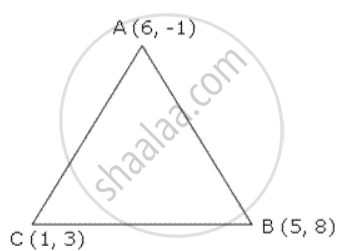
AB = `sqrt ((6 - 5)^2 + (-1-8)^2) = sqrt (1 + 81) = sqrt 82` units
BC = `sqrt ((5-1)^2 + (8 - 3)^2) = sqrt (16+25) = sqrt 41` units
AC = `sqrt ((1-6)^2 + (3 - 1)^2) = sqrt (25 + 16) = sqrt 41` units
∵ BC = AC
∴ A , B and C are the vertices of an isosceles triangle.
APPEARS IN
संबंधित प्रश्न
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
ABC is a triangle and G(4, 3) is the centroid of the triangle. If A = (1, 3), B = (4, b) and C = (a, 1), find ‘a’ and ‘b’. Find the length of side BC.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is ______.
Find the distance between the following point :
(sec θ , tan θ) and (- tan θ , sec θ)
Find the coordinates of O, the centre passing through A( -2, -3), B(-1, 0) and C(7, 6). Also, find its radius.
In what ratio does the point P(−4, y) divides the line segment joining the points A(−6, 10) and B(3, −8)? Hence find the value of y.
Give the relation that must exist between x and y so that (x, y) is equidistant from (6, -1) and (2, 3).
The distance between point P(2, 2) and Q(5, x) is 5 cm, then the value of x ______
The distance between the points A(0, 6) and B(0, -2) is ______.
The distance of the point (5, 0) from the origin is ______.
