Advertisements
Advertisements
प्रश्न
Prove that the points (7 , 10) , (-2 , 5) and (3 , -4) are vertices of an isosceles right angled triangle.
उत्तर
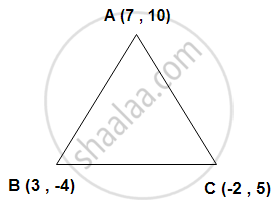
AB = `sqrt ((7 + 2)^2 + (10 - 5)^2) = sqrt (81 + 25) = sqrt 106` units
BC = `sqrt ((-2-3)^2 + (5 + 4)^2) = sqrt (25 + 81) = sqrt 106` units
AC = `sqrt ((7 - 3)^2 + (10 + 4)^2) = sqrt (16 + 196) = sqrt 212` units
∵ AB = BC
∴ ABC is an isosceleles triangle
AB2 + BC2 = 100 + 106 = 212
AC2 = 212
∵ AB2 + BC2 = AC2
∴ ABC is also a right angled triangle.
APPEARS IN
संबंधित प्रश्न
Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (−3, 4).
Find the distance between the points
P(a + b,a - b)andQ(a -b,a + b)
Find the distance between the following pairs of point.
W `((- 7)/2 , 4)`, X (11, 4)
Prove that the following set of point is collinear :
(5 , 5),(3 , 4),(-7 , -1)
Show that the points (2, 0), (–2, 0), and (0, 2) are the vertices of a triangle. Also, a state with the reason for the type of triangle.
Find distance between point A(7, 5) and B(2, 5)
Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle
Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
Find the value of a, if the distance between the points A(–3, –14) and B(a, –5) is 9 units.
