Advertisements
Advertisements
Question
Determine whether the point is collinear.
R(0, 3), D(2, 1), S(3, –1)
Solution
R(0, 3), D(2, 1), S(3, –1)
RD = \[\sqrt{\left( 2 - 0 \right)^2 + \left( 1 - 3 \right)^2}\]
= `sqrt((2)^2 + (- 2)^2)`
= `sqrt(4 + 4)`
= `sqrt8`
= `sqrt(4 xx 2)`
= `2sqrt2`
DS = `sqrt((3 - 2)^2 + ((-1) - 1)^2)`
= `sqrt((1)^2 + (-2)^2)`
= `sqrt(1 + 4)`
= `sqrt5`
RS = `sqrt((3 - 0)^2 + ((-1) - 3)^2)`
= `sqrt((3)^2 + (-4)^2)`
\[ = \sqrt{9 + 16}\]
\[ = \sqrt{25}\]
\[ = 5\]
Sum of two sides is not equal to the third side.
Hence, the given points are not collinear.
APPEARS IN
RELATED QUESTIONS
If the point (x, y) is equidistant from the points (a + b, b – a) and (a – b, a + b), prove that bx = ay
Find the distance between the following pairs of points:
(2, 3), (4, 1)
If the points (2, 1) and (1, -2) are equidistant from the point (x, y), show that x + 3y = 0.
If A (-1, 3), B (1, -1) and C (5, 1) are the vertices of a triangle ABC, find the length of the median through A.
Find the distance between the following pair of points.
R(0, -3), S(0, `5/2`)
If the point P(2, 1) lies on the line segment joining points A(4, 2) and B(8, 4), then ______.
Find the relation between a and b if the point P(a ,b) is equidistant from A (6,-1) and B (5 , 8).
Prove that the points (1 , 1) , (-1 , -1) and (`- sqrt 3 , sqrt 3`) are the vertices of an equilateral triangle.
From the given number line, find d(A, B):

Show that (-3, 2), (-5, -5), (2, -3) and (4, 4) are the vertices of a rhombus.
Given A = (x + 2, -2) and B (11, 6). Find x if AB = 17.
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
Find distance CD where C(– 3a, a), D(a, – 2a)
Show that P(– 2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle
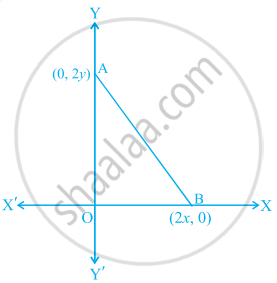
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
If (a, b) is the mid-point of the line segment joining the points A(10, –6) and B(k, 4) and a – 2b = 18, find the value of k and the distance AB.
|
Case Study Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites. |
- Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower.
- After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(`sqrt(3)` - 1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower?

