Advertisements
Advertisements
Question
KM is a straight line of 13 units If K has the coordinate (2, 5) and M has the coordinates (x, – 7) find the possible value of x.
Solution
Using distance formula
(x2 - x1)2 + (y2 - y1)2 = d2
⇒ (x - 2)2 + (-7 - 5)2 = 132
⇒ x2 - 4x + 4 + 144 = 169
⇒ x2 - 4x + 148 - 169 = 0
⇒ x2 - 4x - 21 = 0
⇒ x2 - 7x + 3x - 21 = 0
⇒ (x - 7) +3 (x - 7) = 0
⇒ (x + 3) (x - 7) = 0
x = 7, -3.
APPEARS IN
RELATED QUESTIONS
Find the distance between the following pairs of points:
(a, b), (−a, −b)
Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(- 1, - 2), (1, 0), (- 1, 2), (- 3, 0)
If the point P(2, 1) lies on the line segment joining points A(4, 2) and B(8, 4), then ______.
Find the distance between the following point :
(Sin θ - cosec θ , cos θ - cot θ) and (cos θ - cosec θ , -sin θ - cot θ)
The points A (3, 0), B (a, -2) and C (4, -1) are the vertices of triangle ABC right angled at vertex A. Find the value of a.
If the point (x, y) is at equidistant from the point (a + b, b – a) and (a-b, a + b). Prove that ay = bx.
Find distance between point A(–1, 1) and point B(5, –7):
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = – 7
Using distance formula,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(A, B) = `sqrt(square +[(-7) + square]^2`
∴ d(A, B) = `sqrt(square)`
∴ d(A, B) = `square`
Case Study -2
A hockey field is the playing surface for the game of hockey. Historically, the game was played on natural turf (grass) but nowadays it is predominantly played on an artificial turf.
It is rectangular in shape - 100 yards by 60 yards. Goals consist of two upright posts placed equidistant from the centre of the backline, joined at the top by a horizontal crossbar. The inner edges of the posts must be 3.66 metres (4 yards) apart, and the lower edge of the crossbar must be 2.14 metres (7 feet) above the ground.
Each team plays with 11 players on the field during the game including the goalie. Positions you might play include -
- Forward: As shown by players A, B, C and D.
- Midfielders: As shown by players E, F and G.
- Fullbacks: As shown by players H, I and J.
- Goalie: As shown by player K.
Using the picture of a hockey field below, answer the questions that follow:
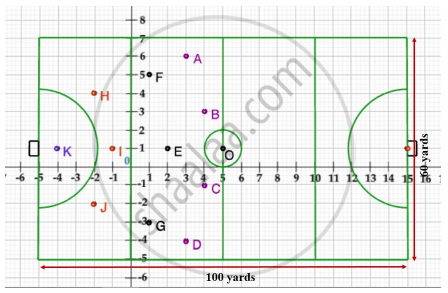
If a player P needs to be at equal distances from A and G, such that A, P and G are in straight line, then position of P will be given by ______.
The distance of the point P(–6, 8) from the origin is ______.
The point A(2, 7) lies on the perpendicular bisector of line segment joining the points P(6, 5) and Q(0, – 4).
