Advertisements
Advertisements
Question
If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
Advertisements
Solution
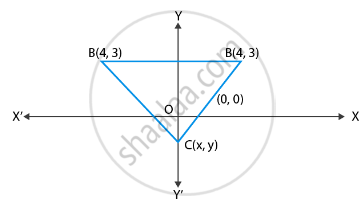
Let the vertices be (x, y)
Distance between (x, y) and (4, 3) is = `sqrt((x - 4)^2 + (y - 3)^2)` ...(1)
Distance between (x,y) and (– 4, 3) is = `sqrt((x + 4)^2 + (y - 3)^2)` ...(2)
Distance between (4, 3) and (– 4, 3) is = `sqrt((4 + 4)^2 + (3 - 3)^2) = sqrt(8)^2`= 8
According to the question,
Equation (1) = (2)
(x – 4)2 = (x + 4)2
x2 – 8x + 16 = x2 + 8x + 16
16x = 0
x = 0
Also, equation (1) = 8
(x – 4)2 + (y – 3)2 = 64 ...(3)
Substituting the value of x in (3)
Then (0 – 4)2 + (y – 3)2 = 64
(y – 3)2 = 64 – 16
(y – 3)2 = 48
y – 3 = `(+)4sqrt(3)`
y = `3(+) 4sqrt(3)`
Neglect y = `3(+) 4sqrt(3)` as if y = `3(+) 4sqrt(3)` then origin cannot interior of triangle
Therefore, the third vertex = `(0, 3 - 4sqrt(3))`
APPEARS IN
RELATED QUESTIONS
If the point P(x, y) is equidistant from the points A(a + b, b – a) and B(a – b, a + b). Prove that bx = ay.
Show that the points (a, a), (–a, –a) and (– √3 a, √3 a) are the vertices of an equilateral triangle. Also find its area.
The value of 'a' for which of the following points A(a, 3), B (2, 1) and C(5, a) a collinear. Hence find the equation of the line.
The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
Find the distance of the following points from the origin:
(ii) B(-5,5)
Find value of x for which the distance between the points P(x,4) and Q(9,10) is 10 units.
If the point A(x,2) is equidistant form the points B(8,-2) and C(2,-2) , find the value of x. Also, find the value of x . Also, find the length of AB.
Show that the points A(1, 2), B(1, 6), C(1 + 2`sqrt3`, 4) are vertices of an equilateral triangle.
Find the distances between the following point.
R(–3a, a), S(a, –2a)
Find the distance of the following point from the origin :
(8 , 15)
The centre of a circle passing through P(8, 5) is (x+l , x-4). Find the coordinates of the centre if the diameter of the circle is 20 units.
Prove that the points (a, b), (a + 3, b + 4), (a − 1, b + 7) and (a − 4, b + 3) are the vertices of a parallelogram.
Prove that the points (0 , -4) , (6 , 2) , (3 , 5) and (-3 , -1) are the vertices of a rectangle.
Find a point on the y-axis which is equidistant from the points (5, 2) and (-4, 3).
Show that the points A (5, 6), B (1, 5), C (2, 1) and D (6, 2) are the vertices of a square ABCD.
Find the point on y-axis whose distances from the points A (6, 7) and B (4, -3) are in the ratio 1: 2.
Find distance between point A(–1, 1) and point B(5, –7):
Solution: Suppose A(x1, y1) and B(x2, y2)
x1 = –1, y1 = 1 and x2 = 5, y2 = – 7
Using distance formula,
d(A, B) = `sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2`
∴ d(A, B) = `sqrt(square +[(-7) + square]^2`
∴ d(A, B) = `sqrt(square)`
∴ d(A, B) = `square`
Show that A(1, 2), (1, 6), C(1 + 2 `sqrt(3)`, 4) are vertices of a equilateral triangle
The point P(–2, 4) lies on a circle of radius 6 and centre C(3, 5).
|
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
|
Based on the above information answer the following questions using the coordinate geometry.
- Find the distance between Lucknow (L) to Bhuj (B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P)
[OR]
Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).
