Advertisements
Advertisements
प्रश्न
If (– 4, 3) and (4, 3) are two vertices of an equilateral triangle, find the coordinates of the third vertex, given that the origin lies in the interior of the triangle.
Advertisements
उत्तर
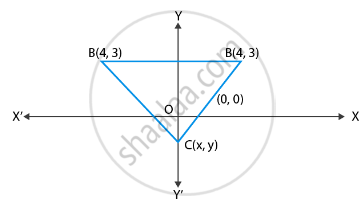
Let the vertices be (x, y)
Distance between (x, y) and (4, 3) is = `sqrt((x - 4)^2 + (y - 3)^2)` ...(1)
Distance between (x,y) and (– 4, 3) is = `sqrt((x + 4)^2 + (y - 3)^2)` ...(2)
Distance between (4, 3) and (– 4, 3) is = `sqrt((4 + 4)^2 + (3 - 3)^2) = sqrt(8)^2`= 8
According to the question,
Equation (1) = (2)
(x – 4)2 = (x + 4)2
x2 – 8x + 16 = x2 + 8x + 16
16x = 0
x = 0
Also, equation (1) = 8
(x – 4)2 + (y – 3)2 = 64 ...(3)
Substituting the value of x in (3)
Then (0 – 4)2 + (y – 3)2 = 64
(y – 3)2 = 64 – 16
(y – 3)2 = 48
y – 3 = `(+)4sqrt(3)`
y = `3(+) 4sqrt(3)`
Neglect y = `3(+) 4sqrt(3)` as if y = `3(+) 4sqrt(3)` then origin cannot interior of triangle
Therefore, the third vertex = `(0, 3 - 4sqrt(3))`
APPEARS IN
संबंधित प्रश्न
Show that four points (0, – 1), (6, 7), (–2, 3) and (8, 3) are the vertices of a rectangle. Also, find its area
Find the distance between the points
A(1,-3) and B(4,-6)
Find the distance between the points:
P(a + b, a - b) and Q(a - b, a + b)
Using the distance formula, show that the given points are collinear:
(-2, 5), (0,1) and (2, -3)
Determine whether the point is collinear.
R(0, 3), D(2, 1), S(3, –1)
Find the distance of the following point from the origin :
(6 , 8)
Find the distance between the following point :
(sec θ , tan θ) and (- tan θ , sec θ)
Find the relation between x and y if the point M (x,y) is equidistant from R (0,9) and T (14 , 11).
The centre of a circle passing through P(8, 5) is (x+l , x-4). Find the coordinates of the centre if the diameter of the circle is 20 units.
Prove that the points (0 , -4) , (6 , 2) , (3 , 5) and (-3 , -1) are the vertices of a rectangle.
Show that the points A (5, 6), B (1, 5), C (2, 1) and D (6, 2) are the vertices of a square ABCD.
The distances of point P (x, y) from the points A (1, - 3) and B (- 2, 2) are in the ratio 2: 3.
Show that: 5x2 + 5y2 - 34x + 70y + 58 = 0.
The point which divides the lines segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
If the distance between the points (4, P) and (1, 0) is 5, then the value of p is ______.
The distance between the point P(1, 4) and Q(4, 0) is ______.
The equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is ______.
What type of a quadrilateral do the points A(2, –2), B(7, 3), C(11, –1) and D(6, –6) taken in that order, form?
If (a, b) is the mid-point of the line segment joining the points A(10, –6) and B(k, 4) and a – 2b = 18, find the value of k and the distance AB.
The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, – 9) and has diameter `10sqrt(2)` units.
