Advertisements
Advertisements
Question
Find distance between points P(– 5, – 7) and Q(0, 3).
By distance formula,
PQ = `sqrt(square + (y_2 - y_1)^2`
= `sqrt(square + square)`
= `sqrt(square + square)`
= `sqrt(square + square)`
= `sqrt(125)`
= `5sqrt(5)`
Solution
By distance formula,
PQ = `sqrt(bb((x^2 - x_1)^2) + (y_2 - y_1)^2`
= `sqrt(bb(0 - (-5)^2) + bb(3 - (-7)^2))`
= `sqrt(bb((5)^2) + bb((10)^2))`
= `sqrt(bb25 + bb100)`
= `sqrt(125)`
= `5sqrt(5)`
APPEARS IN
RELATED QUESTIONS
Determine if the points (1, 5), (2, 3) and (−2, −11) are collinear.
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.

Find the distance between the following pair of points:
(-6, 7) and (-1, -5)
Using the distance formula, show that the given points are collinear:
(-1, -1), (2, 3) and (8, 11)
The long and short hands of a clock are 6 cm and 4 cm long respectively. Find the sum of the distances travelled by their tips in 24 hours. (Use π = 3.14) ?
Determine whether the points are collinear.
L(–2, 3), M(1, –3), N(5, 4)
If the point P(2, 1) lies on the line segment joining points A(4, 2) and B(8, 4), then ______.
Find the distance between the following pair of point in the coordinate plane.
(1 , 3) and (3 , 9)
Find the distance of a point (7 , 5) from another point on the x - axis whose abscissa is -5.
Prove that the points (0 , 0) , (3 , 2) , (7 , 7) and (4 , 5) are the vertices of a parallelogram.
Find the distance between the following pairs of points:
(-3, 6) and (2, -6)
Find the distance between the origin and the point:
(-8, 6)
Find the co-ordinates of points on the x-axis which are at a distance of 17 units from the point (11, -8).
Calculate the distance between A (7, 3) and B on the x-axis whose abscissa is 11.
Show that the points (a, a), (-a, -a) and `(-asqrt(3), asqrt(3))` are the vertices of an equilateral triangle.
If the point (x, y) is at equidistant from the point (a + b, b – a) and (a-b, a + b). Prove that ay = bx.
If the length of the segment joining point L(x, 7) and point M(1, 15) is 10 cm, then the value of x is ______
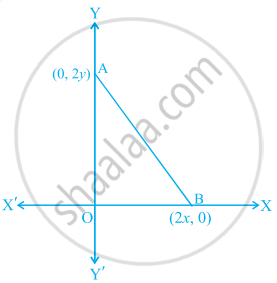
The coordinates of the point which is equidistant from the three vertices of the ΔAOB as shown in the figure is ______.
Find the value of a, if the distance between the points A(–3, –14) and B(a, –5) is 9 units.
The centre of a circle is (2a, a – 7). Find the values of a if the circle passes through the point (11, – 9) and has diameter `10sqrt(2)` units.
