Advertisements
Advertisements
Question
In a classroom, 4 friends are seated at the points A, B, C and D as shown in the following figure. Champa and Chameli walk into the class and after observing for a few minutes, Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees.
Using distance formula, find which of them is correct.

Solution
It can be observed that A (3, 4), B (6, 7), C (9, 4), and D (6, 1) are the positions of these 4 friends.
AB = `sqrt((3-6)^2+(4-7)^2)`
= `sqrt((-3)^2+(-3)^2)`
= `sqrt(9+9)`
= `sqrt18`
= `3sqrt2`
BC = `sqrt((6-9)^2+(7-4)^2) `
= `sqrt((-3)^2+(3)^2)`
= `sqrt(9+9)`
= `sqrt18`
= `3sqrt2`
CD = `sqrt((9-6)^2+(4-1)^2)`
= `sqrt((3)^2+(3)^2)`
= `sqrt(9+9)`
= `sqrt18`
= `3sqrt2`
AD = `sqrt((3-6)^2+(4-1)^2)`
= `sqrt((-3)^2 + (3)^2)`
= `sqrt(9+9)`
= `sqrt18`
= `3sqrt2`
Diagonal AC = `sqrt((3-9)^2+(4-4)^2)`
= `sqrt((-6)^2)`
= 6
Diagonal BD = `sqrt((6-6)^2+(7-1)^2)`
= `sqrt((6)^2)`
= 6
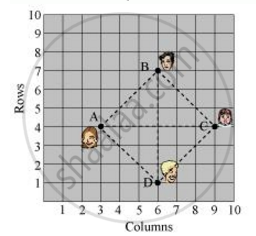
It can be observed that all sides of this quadrilateral ABCD are of the same length and also the diagonals are of the same length.
Therefore, ABCD is a square and hence, Champa was correct.
APPEARS IN
RELATED QUESTIONS
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, –5) and R(–3, 6), find the coordinates of P.
If P and Q are two points whose coordinates are (at2 ,2at) and (a/t2 , 2a/t) respectively and S is the point (a, 0). Show that `\frac{1}{SP}+\frac{1}{SQ}` is independent of t.
If the distance between the points (4, k) and (1, 0) is 5, then what can be the possible values of k?
Find the circumcenter of the triangle whose vertices are (-2, -3), (-1, 0), (7, -6).
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3)
Find the distance between the points
A(1,-3) and B(4,-6)
Find the distance of the following points from the origin:
(i) A(5,- 12)
Find the distance of the following point from the origin :
(0 , 11)
P and Q are two points lying on the x - axis and the y-axis respectively . Find the coordinates of P and Q if the difference between the abscissa of P and the ordinates of Q is 1 and PQ is 5 units.
The centre of a circle passing through P(8, 5) is (x+l , x-4). Find the coordinates of the centre if the diameter of the circle is 20 units.
Find the distance between the origin and the point:
(-8, 6)
A point P lies on the x-axis and another point Q lies on the y-axis.
If the abscissa of point P is -12 and the ordinate of point Q is -16; calculate the length of line segment PQ.
Given A = (3, 1) and B = (0, y - 1). Find y if AB = 5.
The centre of a circle is (2x - 1, 3x + 1). Find x if the circle passes through (-3, -1) and the length of its diameter is 20 unit.
The length of line PQ is 10 units and the co-ordinates of P are (2, -3); calculate the co-ordinates of point Q, if its abscissa is 10.
Give the relation that must exist between x and y so that (x, y) is equidistant from (6, -1) and (2, 3).
Show that the points (0, –1), (8, 3), (6, 7) and (– 2, 3) are vertices of a rectangle.
The point which divides the lines segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the ______.
Points A(4, 3), B(6, 4), C(5, –6) and D(–3, 5) are the vertices of a parallelogram.
