Advertisements
Advertisements
प्रश्न
For a surface molecule ______.
- the net force on it is zero.
- there is a net downward force.
- the potential energy is less than that of a molecule inside.
- the potential energy is more than that of a molecule inside.
उत्तर
b and d
Explanation:
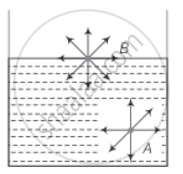
Consider the diagram where two molecules of a liquid are shown. One is well inside the liquid and the other is on the surface. The molecule (A) which is well inside experiences equal forces from all directions, hence net force on it will be zero.
And molecules on the liquid surface have some extra energy as it surrounded surround by only the lower half side of the liquid molecules.
APPEARS IN
संबंधित प्रश्न
'n' droplets of equal size of radius r coalesce to form a bigger drop of radius R. The energy liberated is equal to...................
(T =Surface tension of water)
`(a) 4piR^2T[n^(1/3)-1]`
`(b) 4pir^2T[n^(1/3)-1]`
`(c) 4piR^2T[n^(2/3)-1]`
`(d)4 pir^2T[n^(2/3)-1]`
In a conical pendulum, a string of length 120 cm is fixed at rigid support and carries a mass
of 150 g at its free end. If the mass is revolved in a horizontal circle of radius 0.2 m around a
vertical axis, calculate tension in the string (g = 9.8 m/s2)
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
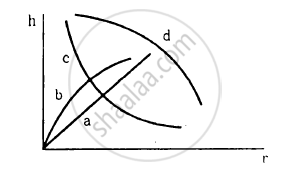
Which of the following graphs may represent the relation between the capillary rise hand the radius r of the capillary?
Viscosity is a property of
A 5.0 cm long straight piece of thread is kept on the surface of water. Find the force with which the surface on one side of the thread pulls it. Surface tension of water = 0.076 N m−1.
Two soap bubbles have a radius in the ratio of 2:3. Compare the works done in blowing these bubbles.
The excess of pressure, due to surface tension, on a spherical liquid drop of radius 'R' is proportional to ______.
A molecule of water on the surface experiences a net ______.
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
