Advertisements
Advertisements
प्रश्न
For the reaction, \[\ce{A2(g) + B2(g) <=> 2AB(g); \Delta H}\] is -ve.
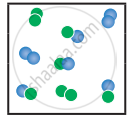
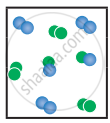
the following molecular scenes represent differenr reaction mixture. (A-green, B-blue)
| Closed ← |
 |
 |
 |
| System | At equilibrium | (x) | (y) |
- Calculate the equilibrium constant Kp and (Kc).
- For the reaction mixture represented by scene (x), (y) the reaction proceed in which directions?
- What is the effect of an increase in pressure for the mixture at equilibrium?
उत्तर
Kc = `(["AB"]^2)/(["A"_2]["B"_2])`; A – green, B – blue
Given that ‘V’ is constant(closed system)
At equilbrium,
Kc = `((-))/((2/"V")(2/"V")) = 16/4 = 4`
Kp = Kc(RT)∆n = 4 (RT)0 = 4
At stage ‘x’,
Q = `((6/"V")^2)/((2/"V")(1/"V")) = 36/2 = 18`
Q > Kc i.e., reverse reaction is favoured.
At stage ‘y’,
Q = `((3/"V")^2)/((3/"V")(3/"V")) = 9/(3 xx 3) = 1`
Kc > Q i.e., forward reaction is favoured.
APPEARS IN
संबंधित प्रश्न
For the reaction \[\ce{AB(g) <=> A(g) + B(g)}\], at equilibrium, AB is 20 % dissociated at a total pressure of P, the equilibrium constant Kp is related to the total pressure by the expression
The values of Kp1 and Kp2; for the reactions,
X ⇌ Y + Z,
A ⇌ 2B are in the ratio 9 : 1 if degree of dissociation of X and A be equal then total pressure at equilibrium P1, and P2 are in the ratio
For the formation of Two moles of SO3(g) from SO2 and O2, the equilibrium constant is K1. The equilibrium constant for the dissociation of one mole of SO3 into SO2 and O2 is
The equilibrium constants of the following reactions are:
\[\ce{N2 + 3H2 <=> 2NH3}\]; K1
\[\ce{N2 + O2 <=> 2NO}\]; K2
\[\ce{H2 + 1/2O2 <=> H2O}\]; K3
The equilibrium constant (K) for the reaction;
\[\ce{2NH3 + 5/2 O2 <=> 2NO + 3H2O}\], will be
Derive a general expression for the equilibrium constant Kp and Kc for the reaction, \[\ce{3H2(g) + N2(g) <=> 2NH3(g)}\].
What is the effect of added Inert gas on the reaction at equilibrium?
Derive the relation between Kp and Kc.
At particular temperature Kc = 4 × 10-2 for the reaction, \[\ce{H2S (g) <=> H2(g) +1/2 S2(g)}\]. Calculate the Kc for the following reaction.
\[\ce{2H2S (g) <=> 2H2 (g) + S2 (g)}\]
The equilibrium for the dissociation of XY2 is given as,
\[\ce{2 XY2 (g) <=> 2 XY (g) + Y2 (g)}\]
if the degree of dissociation x is so small compared to one. Show that 2 Kp = PX3 where P is the total pressure and Kp is the dissociation equilibrium constant of XY2.
The partial pressure of carbon dioxide in the reaction
\[\ce{CaCO3(s) <=> CaO(s) + CO2(g)}\] is 1.017 × 10-3 atm at 500°C. Calculate Kp at 600°C for the reaction. H for the reaction is 181 KJ mol-1 and does not change in the given range of temperature.
