Advertisements
Advertisements
प्रश्न
For what value of k, −4 is a zero of the polynomial x2 − x − (2k + 2)?
उत्तर
We know that if x = a is zero polynomial then x - 2 is a factor of f(x)
Since -4 is zero of f(x)
Therefore x+ 4 is a factor of f(x)
Now, we divide `f(x)= x^ -x -(2 k+ 2 )` by ` g(x)= x+ 2` to find the value of k
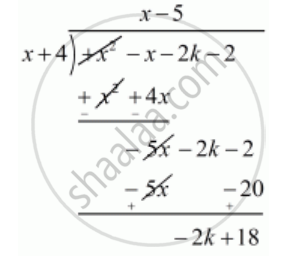
Now, Remainder = 0
` -2k + 18 =0`
` - 2k = -18`
` k = (-18)/(-2)`
`k = (cancel(-)18)/(cancel(-)2)`
k = 9
Hence, the value of k is 9
APPEARS IN
संबंधित प्रश्न
If the product of zeros of the quadratic polynomial f(x) = x2 − 4x + k is 3, find the value of k.
State division algorithm for polynomials.
For what value of k, is −2 a zero of the polynomial 3x2 + 4x + 2k?
If the graph of quadratic polynomial ax2 + bx + c cuts negative direction of y-axis, then what is the sign of c?
If α, β are the zeros of the polynomial f(x) = x2 + x + 1, then \[\frac{1}{\alpha} + \frac{1}{\beta} =\]
Identify the following expression is polynomial. If not give reason:
`1/(x^(-2)) + 1/(x^(-1)) + 7`
The number of polynomials having zeroes as 4 and 7 is ______.
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

The graph of parabola opens upwards, if:
`sqrt(2)` is a polynomial of degree ______.
Classify the following as a constant, linear, quadratic and cubic polynomials:
`sqrt(2)x - 1`
