Advertisements
Advertisements
प्रश्न
If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
उत्तर
Given,
p(x) = ax2 − 3(a − 1) x − 1
Zero is 1
Now,
p(1) = a(1)2 – 3(a – 1) ×1 – 1 = 0
p(1) = a – 3a + 3 – 1 = 0
p(1) = – 2a + 2 = 0
= – 2a = – 2
= a = `(-2)/-2 = 1`
So the value of a = 1
APPEARS IN
संबंधित प्रश्न
If x = 3 is one root of the quadratic equation x2 – 2kx – 6 = 0, then find the value of k.
Classify the following polynomials as polynomials in one-variable, two variables etc:
`x^2-2tx+7t^2-x+t`
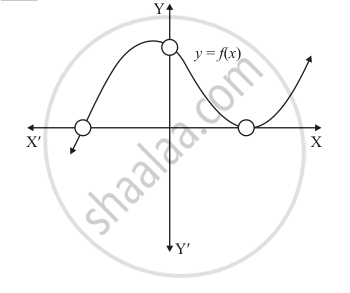
The graph of a polynomial y = f(x), shown in Fig. 2.18. Find the number of real zeros of f(x).
Write the coefficient of the polynomial p(z) = z5 − 2z2 + 4.
If α, β are the zeros of the polynomial 2y2 + 7y + 5, write the value of α + β + αβ.
Obtain all the zeroes of the polynomial 2x4 − 5x3 − 11x2 + 20x + 12 when 2 and − 2 are two zeroes of the above polynomial.
Identify the following expression is polynomial. If not give reason:
`"m"^2 - root(3)("m") + 7"m" - 10`
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If the roots of the quadratic polynomial are equal, where the discriminant D = d2 – 4ac, then:
`sqrt(2)` is a polynomial of degree ______.
Classify the following as a constant, linear, quadratic and cubic polynomials:
`5t - sqrt(7)`
