Advertisements
Advertisements
प्रश्न
If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
उत्तर
Given,
p(x) = ax2 − 3(a − 1) x − 1
Zero is 1
Now,
p(1) = a(1)2 – 3(a – 1) ×1 – 1 = 0
p(1) = a – 3a + 3 – 1 = 0
p(1) = – 2a + 2 = 0
= – 2a = – 2
= a = `(-2)/-2 = 1`
So the value of a = 1
APPEARS IN
संबंधित प्रश्न
A plane left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`3y`
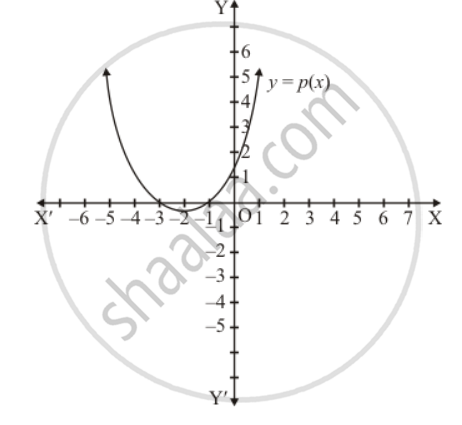
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
For what value of k, −4 is a zero of the polynomial x2 − x − (2k + 2)?
State whether the given algebraic expression are polynomial? Justify.
`y + 1/y`
Let the polynomials be
(A) −13q5 + 4q2 + 12q
(B) (x2 + 4)(x2 + 9)
(C) 4q8 – q6 + q2
(D) `– 5/7 y^12 + y^3 + y^5`
Then ascending order of their degree is
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

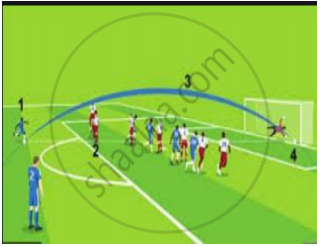
The graph of parabola opens upwards, if:
Degree of the polynomial 4x4 + 0x3 + 0x5 + 5x + 7 is ______.
Determine the degree of the following polynomial:
–10
Classify the following as a constant, linear, quadratic and cubic polynomials:
1 + x + x2
