Advertisements
Advertisements
Question
If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
Solution
Given,
p(x) = ax2 − 3(a − 1) x − 1
Zero is 1
Now,
p(1) = a(1)2 – 3(a – 1) ×1 – 1 = 0
p(1) = a – 3a + 3 – 1 = 0
p(1) = – 2a + 2 = 0
= – 2a = – 2
= a = `(-2)/-2 = 1`
So the value of a = 1
APPEARS IN
RELATED QUESTIONS
Define value of polynomial at a point.
Write the family of quadratic polynomials having \[- \frac{1}{4}\] and 1 as its zeros.
If the sum of the zeros of the quadratic polynomial f(x) = kx2 − 3x + 5 is 1, write the value of k.
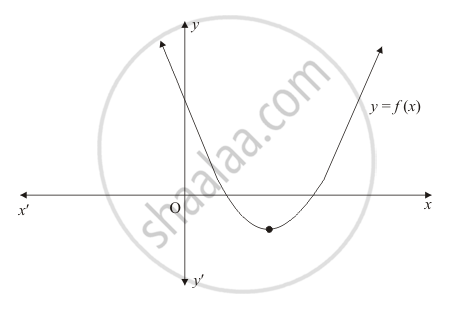
The graph of the polynomial f(x) = ax2 + bx + c is as shown below (Fig. 2.19). Write the signs of 'a' and b2 − 4ac.
If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then \[\frac{1}{\alpha} + \frac{1}{\beta}\] is equal to
If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 − 4x + 9 is 3, then its third zero is
Divide. Write the quotient and the remainder.
(8p3 − 4p2) ÷ 2p2
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




In the standard form of a quadratic polynomial, ax2 + bx + c, a, b and c are:
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the coefficient of x6
If a polynomial p(x) is given by p(x) = x2 - 5x + 6, then the value of p(1) + p(4) is ______.
