Advertisements
Advertisements
Question
The graph of the polynomial f(x) = ax2 + bx + c is as shown below (Fig. 2.19). Write the signs of 'a' and b2 − 4ac.
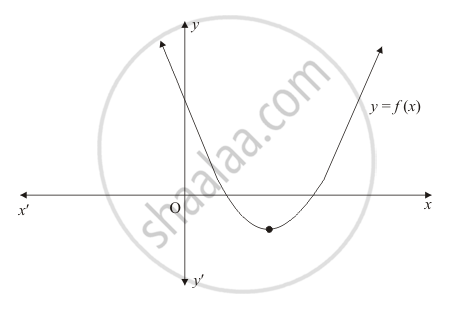
Solution
Clearly, `f(x) = ax^2 bx + c` represent a parabola opening upwards. Therefore, `a > 0`

Since the parabola cuts x-axis at two points, this means that the polynomial will have two real solutions
Hence `b^2 - 4 ac > 0`
Hence ` a> 0 `and `b^2 - 4ac > 0 `
APPEARS IN
RELATED QUESTIONS
Define degree of a polynomial.
If the sum of the zeros of the quadratic polynomial f(x) = kx2 − 3x + 5 is 1, write the value of k.
In Q. No. 14, write the sign of c.
If x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k, write the value of k.
If a − b, a and b are zeros of the polynomial f(x) = 2x3 − 6x2 + 5x − 7, write the value of a.
Let the polynomials be
(A) −13q5 + 4q2 + 12q
(B) (x2 + 4)(x2 + 9)
(C) 4q8 – q6 + q2
(D) `– 5/7 y^12 + y^3 + y^5`
Then ascending order of their degree is
Which of the following is not the graph of quadratic polynomial?
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If the roots of the quadratic polynomial are equal, where the discriminant D = d2 – 4ac, then:
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the constant term
Classify the following as a constant, linear, quadratic and cubic polynomials:
2 – x2 + x3
