Advertisements
Advertisements
Question
If x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k, write the value of k.
Solution
We have to find the value of K if x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k.
`f (x)= x^3 - 2x^2 + 4x + k`
`f(1)= 1^3 -2 (1)^2+ 4 xx1 + k`
`0 = 1 - 2 + 4 + k`
`0 = 5 - 2 + k `
`0 = 3 + k`
` - 3 = k `
Hence, the value of k is k = - 3
APPEARS IN
RELATED QUESTIONS
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`3x-2`
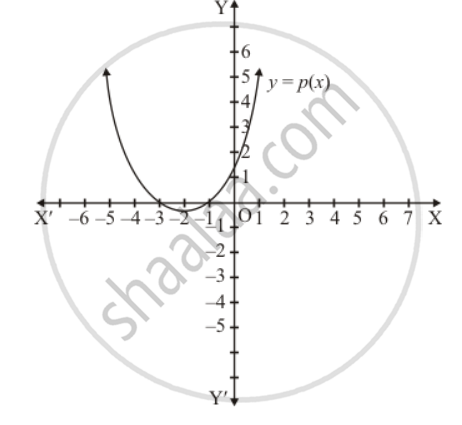
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are coincident. (True/False).
Figure 2.23 show the graph of the polynomial f(x) = ax2 + bx + c for which

If the product of zeros of the polynomial f(x) ax3 − 6x2 + 11x − 6 is 4, then a =
Divide. Write the quotient and the remainder.
(8p3 − 4p2) ÷ 2p2
Find the quadratic polynomial, sum, and product of whose zeroes are −1 and −20 respectively. Also, find the zeroes of the polynomial so obtained.
Let the polynomials be
(A) −13q5 + 4q2 + 12q
(B) (x2 + 4)(x2 + 9)
(C) 4q8 – q6 + q2
(D) `– 5/7 y^12 + y^3 + y^5`
Then ascending order of their degree is
Case Study -1

The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time ‘t’ in seconds is given by the polynomial h(t) such that h(t) = -16t2 + 8t + k.
A polynomial q(t) with sum of zeroes as 1 and the product as -6 is modelling Anu’s height in feet above the water at any time t( in seconds). Then q(t) is given by ______.
