Advertisements
Advertisements
Question
The graph of a polynomial f(x) is as shown in Fig. 2.21. Write the number of real zeros of f(x).
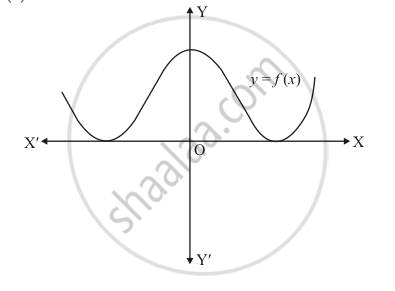
Solution
The graph of a polynomial `F(x)` touches x−axis at two points
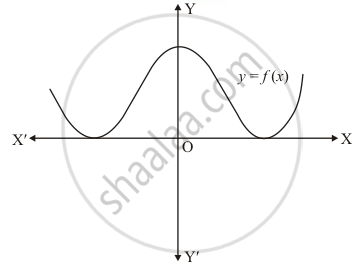
We know that if a curve touches the x-axis at two points then it has two common zeros of `f(x)`.
Hence the number of zeros of `f (x )`, in this case is 2.
APPEARS IN
RELATED QUESTIONS
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials
`7t^4+4t^3+3t-2`
Write the standard form of a linear polynomial with real coefficients.
If x = 1 is a zero of the polynomial f(x) = x3 − 2x2 + 4x + k, write the value of k.
Write the zeros of the polynomial x2 − x − 6.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f(x)?
If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are coincident. (True/False).
If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then \[\frac{1}{\alpha} + \frac{1}{\beta}\] is equal to
If the product of zeros of the polynomial f(x) ax3 − 6x2 + 11x − 6 is 4, then a =
Classify the following as a constant, linear, quadratic and cubic polynomials:
4 – 5y2
Classify the following as a constant, linear, quadratic and cubic polynomials:
y3 – y
