Advertisements
Advertisements
Question
If the product of zeros of the polynomial f(x) ax3 − 6x2 + 11x − 6 is 4, then a =
Options
\[\frac{3}{2}\]
\[- \frac{3}{2}\]
\[\frac{2}{3}\]
\[- \frac{2}{3}\]
\[- \frac{2}{3}\]
Solution
Since `alpha` and`beta` are the zeros of quadratic polynomial f(x) ax3 − 6x2 + 11x − 6
`alpha + ß = - (text{coefficient of x})/(text{coefficient of } x^2)`
So we have
`4 = ((-6)/a)`
`4 = 6/a`
`4a=6`
`a = 6/4`
`a= (3xxcancel(2))/(2xxcancel(2))`
`a = 3/2`
The value of a is `3/2`
Hence, the correct alternative is (a).
APPEARS IN
RELATED QUESTIONS
Write the family of quadratic polynomials having \[- \frac{1}{4}\] and 1 as its zeros.
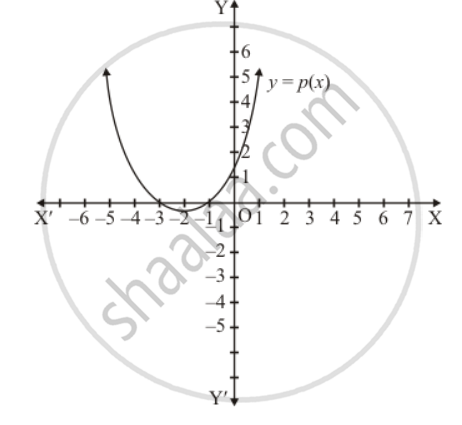
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
State division algorithm for polynomials.
If α, β are the zeros of the polynomial 2y2 + 7y + 5, write the value of α + β + αβ.
If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then \[\frac{1}{\alpha} + \frac{1}{\beta}\] is equal to
If the diagram in Fig. 2.22 shows the graph of the polynomial f(x) = ax2 + bx + c, then

Divide. Write the quotient and the remainder.
(8p3 − 4p2) ÷ 2p2
Identify the following expression is polynomial. If not give reason:
`1/x^2 + 3x - 4`
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




If the roots of the quadratic polynomial are equal, where the discriminant D = d2 – 4ac, then:
The degree of the sum of two polynomials each of degree 5 is always 5.
