Advertisements
Advertisements
प्रश्न
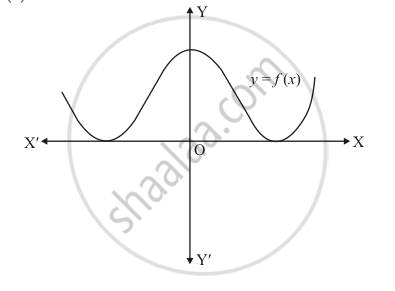
The graph of a polynomial f(x) is as shown in Fig. 2.21. Write the number of real zeros of f(x).
उत्तर
The graph of a polynomial `F(x)` touches x−axis at two points
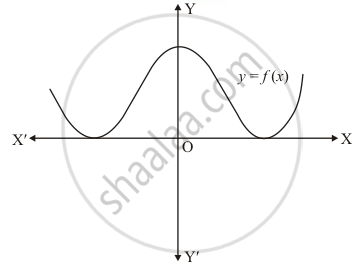
We know that if a curve touches the x-axis at two points then it has two common zeros of `f(x)`.
Hence the number of zeros of `f (x )`, in this case is 2.
APPEARS IN
संबंधित प्रश्न
If 1 is a zero of the polynomial p(x) = ax2 − 3(a − 1) x − 1, then find the value of a.
If α, β are the zeros of the polynomial 2y2 + 7y + 5, write the value of α + β + αβ.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f(x)?
If α, β are the zeros of the polynomial f(x) = x2 − p(x + 1) − c such that (α +1) (β + 1) = 0, then c =
Figure 2.23 show the graph of the polynomial f(x) = ax2 + bx + c for which

If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 − 4x + 9 is 3, then its third zero is
If Q.No. 14, c =
State whether the given algebraic expression are polynomial? Justify.
`2 - 5 sqrt x`
Identify the following expression is polynomial. If not give reason:
x2(x – 1)
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the constant term
