Advertisements
Advertisements
प्रश्न
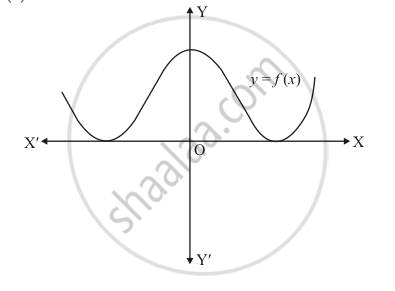
The graph of a polynomial f(x) is as shown in Fig. 2.21. Write the number of real zeros of f(x).
उत्तर
The graph of a polynomial `F(x)` touches x−axis at two points
We know that if a curve touches the x-axis at two points then it has two common zeros of `f(x)`.
Hence the number of zeros of `f (x )`, in this case is 2.
APPEARS IN
संबंधित प्रश्न
Write the standard form of a linear polynomial with real coefficients.
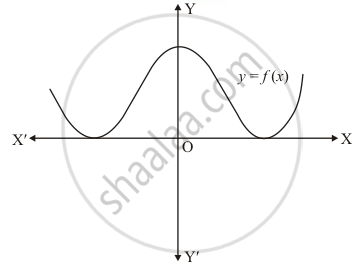
The graph of the polynomial f(x) = ax2 + bx + c is as shown below (Fig. 2.19). Write the signs of 'a' and b2 − 4ac.
If α, β are the zeros of the polynomial f(x) = x2 + x + 1, then \[\frac{1}{\alpha} + \frac{1}{\beta} =\]
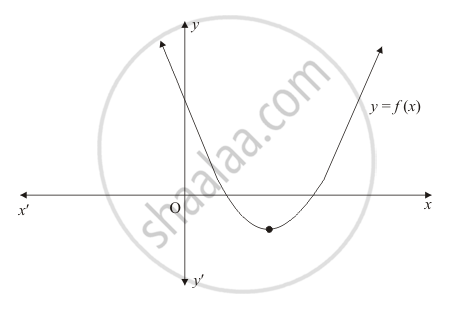
If the diagram in Fig. 2.22 shows the graph of the polynomial f(x) = ax2 + bx + c, then

Which of the following is a polynomial?
Divide. Write the quotient and the remainder.
(21x4 − 14x2 + 7x) ÷ 7x3
Divide. Write the quotient and the remainder.
(6x5 − 4x4 + 8x3 + 2x2) ÷ 2x2
Case Study -1

The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that h(t) = -16t2 + 8t + k.
Rita’s height (in feet) above the water level is given by another polynomial p(t) with zeroes -1 and 2. Then p(t) is given by ______.
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




The graph of x2 + 1 = 0
Classify the following as a constant, linear, quadratic and cubic polynomials:
`5t - sqrt(7)`
