Advertisements
Advertisements
प्रश्न
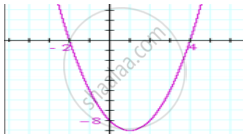
If the diagram in Fig. 2.22 shows the graph of the polynomial f(x) = ax2 + bx + c, then

पर्याय
a > 0, b < 0 and c > 0
a < 0, b < 0 and c < 0
a < 0, b > 0 and c > 0
a < 0, b > 0 and c < 0
उत्तर
Clearly, `f(x) = ax^2 +bx +c` represent a parabola opening upwards.

Therefore, ` a > 0` cuts Y axis at P which lies on `OY`. Putting x = 0 in `y = ax^2 + bx + c`, we get y = c. So the coordinates of P is `(0,c)`. Clearly, P lies on `OY`. Therefore `c < 0`
Hence, the correct choice is `(a)`
APPEARS IN
संबंधित प्रश्न
Write the standard form of a quadratic polynomial with real coefficients.
If a quadratic polynomial f(x) is a square of a linear polynomial, then its two zeros are coincident. (True/False).
Figure 2.23 show the graph of the polynomial f(x) = ax2 + bx + c for which

If the product of two zeros of the polynomial f(x) = 2x3 + 6x2 − 4x + 9 is 3, then its third zero is
Divide. Write the quotient and the remainder.
(6x5 − 4x4 + 8x3 + 2x2) ÷ 2x2
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




In the standard form of a quadratic polynomial, ax2 + bx + c, a, b and c are:
The below picture are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.




The graph of x2 + 1 = 0
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.


The shape of the poses shown is:
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.


The two zeroes in the below shown graph are:
Determine the degree of the following polynomial:
y3(1 – y4)
