Advertisements
Advertisements
प्रश्न
गोलाकार बागेचा व्यास 13 मीटर आहे. बागेच्या दोन दरवाजांमधील अंतरही 13 मीटर आहे. बागेच्या परिघावर विजेचा खांब असा उभारायचा आहे की दोन्ही दरवाजांपासून खांबापर्यंत असणाऱ्या अंतरातील फरक 7 मीटर असायला हवा. असा खांब उभारता येईल का? उत्तर होय असल्यास, प्रत्येक दरवाजापासून खांबापर्यंतचे अंतर काढा.
उत्तर
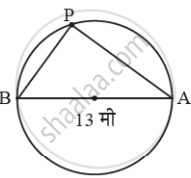
आकृतीमध्ये, A व B बागेचे दरवाजे आणि P म्हणजे विजेचा खांब मानू.
दिलेल्या अटीनुसार,
AP − PB = 7
∴ AP = 7 + PB ...(i)
AB व्यास असल्यामुळे,
∴ ∠APB = 90° ... [व्यास वर्तुळाच्या कोणत्याही बिंदूवर काटकोन निश्चित करतो.]
ΔAPB मध्ये,
AB2 = AP2 + PB2 ...[पायथागोरसचे प्रमेय]
∴ 132 = (7 + PB)2 + PB2 ...[(i) वरून]
PB ला x मानू.
∴ 169 = (7 + x)2 + x2
∴169 = 49 + 14x + x2 + x2
∴ 2x2 + 14x − 120 = 0
∴ x2 + 7x − 60 = 0
∴ x2 + 12x − 5x − 60 = 0
∴ x(x + 12) − 5(x + 12) = 0
∴ (x + 12) (x − 5) = 0
∴ x + 12 = 0 किंवा x − 5 = 0
∴ x = −12 किंवा x = 5
पण अंतर ऋण असू शकत नाही.
∴ x = 5
∴ PB = 5 मीटर
AP = 7 + PB
= 7 + 5
= 12 मीटर
∴ विजेचा खांब उभारता येऊ शकतो. दोन्ही दरवाजांपासून तो 5 मीटर आणि 12 मीटर अंतरावर असेल.
