SSC (Marathi Medium)
Academic Year: 2023-2024
Date & Time: 24th July 2024, 11:00 am
Duration: 2h
Advertisements
- सर्व प्रश्न सोडवणे आवश्यक आहे.
- गणकयंत्राचा वापर करता येणार नाही.
- प्रश्नाच्या उजवीकडे दिलेल्या संख्या पूर्ण गुण दर्शवितात.
- प्रत्येक बहुपर्यायी प्रश्नाच्या उत्तराचे [प्रश्न क्र. 1(अ)] मूल्यमापन केवळ प्रथम प्रयत्नातील पर्याय ग्राह्य धरून केले जाईल व त्यालाच गुण दिले जातील.
- आवश्यक त्या ठिकाणी उत्तराशेजारी आकृती काढावी.
- रचनेच्या सर्व खुणा स्पष्ट असाव्यात. त्या पुसू नयेत.
- प्रमेयाची सिद्धता लिहिण्यासाठी आकृती आवश्यक आहे.
जर ΔABC व ΔPQR मध्ये एका एकास एक संगतीत `"AB"/"QR" = "BC"/"PR" = "CA"/"PQ"` तर खालीलपैकी सत्य विधान कोणते?

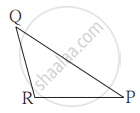
ΔPQR ~ ΔABC
ΔPQR ~ ΔCAB
ΔCBA ~ ΔPQR
ΔBCA ~ ΔPQR
Chapter: [0.01] समरूपता
त्रिज्या अनुक्रमे 5.5 सेमी आणि 3.3 सेमी असलेली दोन वर्तुळे परस्परांना स्पर्श करतात. त्यांच्या केंद्रातील अंतर किती सेमी आहे?
4.4 सेमी
8.8 सेमी
2.2 सेमी
8.3 सेमी
Chapter:
रेख AB, हा Y-अक्षाला समांतर असून A बिंदूचे निर्देशक (1, 3) आहेत तर, B बिंदूचे निर्देशक ______ असू शकतील.
(3, 1)
(5, 3)
(3, 0)
(1, -3)
Chapter: [0.05] निर्देशक भूमिती
10 सेमी बाजू असलेल्या घनाचे घनफळ ______.
1,000 सेमी3
100 सेमी3
10,000 सेमी3
10 सेमी3
Chapter:
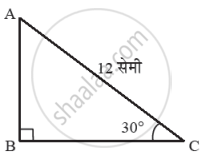
ΔABC मध्ये, ∠B = 90°, ∠C = 30°, AC = 12 सेमी, तर AB काढा.
Chapter:
वर्तुळाची त्रिज्या 4 सेमी असून वर्तुळकंसाची लांबी 10 सेमी आहे, तर वर्तुळपाकळीचे क्षेत्रफळ काढा.
Chapter:
Advertisements
आकृतीत जीवा PQ आणि जीवा RS एकमेकींना बिंदू T मध्ये छेदतात. तर ∠STQ = `1/2`[m(कंस SQ) + m(कंस PR)] हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.
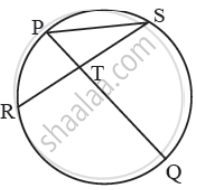
कृती:
∠STQ = ∠SPQ + `square` ...[त्रिकोणाच्या दूरस्थ आंतरकोनांचा प्रमेय]
= `1/2` m(कंस arc SQ) + `square` ...[अंतर्लिखित कोनाचा प्रमेय]
= `1/2 [square + square]`
Chapter:
जर secθ = `25/7`, तर tanθ ची किंमत काढण्यासाठी खालील कृती पूर्ण करा.
कृती:
1 + tan2θ = sec2θ
∴ 1 + tan2θ = `square`
∴ `tan^2θ = 625/49 - square`
∴ `tan^2θ = (625 - 49)/49`
∴ `tan^2θ = (square/49)`
∴ tanθ = `square`
Chapter:
एका शंकूच्या तळाची त्रिज्या 7 सेमी असून त्याची लंब उंची 6 सेमी आहे. तर शंकूचे घनफळ काढण्यासाठी खालील कृती पूर्ण करा.
कृती:
येथे, त्रिज्या (r) = 7 सेमी
उंची (h) = 6 सेमी
∴ शंकूचे घनफळ = `square` ...(सूत्र)
= `1/3 xx 22/7 xx square xx 6`
= `1/3 xx 22/7 xx square xx 6`
∴ शंकूचे घनफळ = `square` सेमी3
Chapter:
केंद्र P व त्रिज्या 3.2 सेमी असलेल्या वर्तुळाला त्यावरील M बिंदूतून स्पर्शिका काढा.
Chapter: [0.04] भौमितिक रचना
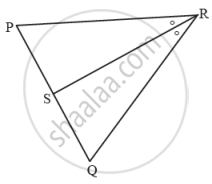
ΔPQR मध्ये, रेख RS हा ∠PRQ चा दुभाजक आहे. जर PR = 15, RQ = 20, PS = 12, तर SQ काढा.
Chapter:
एका गोलाचा व्यास 14 सेमी असेल तर त्याचे पृष्ठफळ काढा.
Chapter:
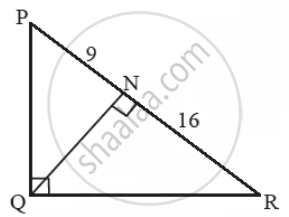
वरील आकृतीत, ∠PQR = 90°, रेख QN ⊥ रेख PR, PN = 9, NR = 16, तर QN काढा.
Chapter:
A(3, 3) आणि B(5, 7) या बिंदूंतून जाणाऱ्या रेषेचा चढ काढा.
Chapter:
Advertisements
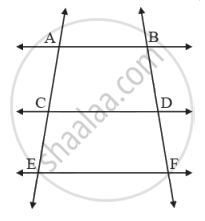
वरील आकृतीत, AB || CD || EF. जर AC = 12, CE = 9, BD = 8, तर DF करण्यासाठी खालील कृती पूर्ण करा.
कृती:
AB || CD || EF
∴ `"AC"/square = square/"DF"` ...(तीन समांतर रेषा व त्यांच्या छेदिका यांचा गुणधर्म)
∴ `12/square = square/"DF"`
∴ DF = `(8 xx 9)/square`
∴ DF = `square`
Chapter:
7 सेमी त्रिज्या आणि 21 सेमी उंची असलेली वृत्तचिती आहे. वृत्तचितीच्या तळाचा परीघ आणि घनफळ काढण्यासाठी खालील कृती पूर्ण करा.
कृती:
त्रिज्या (r) = 7 सेमी
उंची (h) = 21 सेमी
वृत्तचितीचे घनफळ = `square` ...(सूत्र)
= `22/7 xx 7 xx 7 xx square`
= 154 × 21
= `square` सेमी3
तळाचा परीघ = `square` ... [सूत्र]
= `2 xx 22/7 xx square
= square` सेमी
Chapter:
सिद्ध करा 'चक्रीय चौकोनाचे संमुख कोन परस्परांचे पूरककोन असतात.'
Chapter: [0.03] वर्तुळ
P केंद्र व 3.5 सेमी त्रिज्या घेऊन एक वर्तुळ काढा. वर्तुळकेंद्रापासून 8 सेमी अंतरावर Q बिंदू घ्या. Q बिंदूतून वर्तुळाला स्पर्शिका काढा.
Chapter:
P(−2, 3), Q(1, 2), R(4, 1) हे बिंदू एकरेषीय आहेत हे दाखवा.
Chapter:
ΔLMN ~ ΔPQR, 9 × A(ΔPQR) = 16 × A(ΔLMN) जर QR = 20 तर MN काढा.
Chapter: [0.01] समरूपता
ΔABC हा समभूज त्रिकोण आहे. रेख BC वर D बिंदू असा आहे की BD = `1/5` BC, तर `"AD"^2/"AB"^2 = 21/25` हे सिद्ध करा.
Chapter:
ΔLMN ∼ ΔLQP. ΔLMN मध्ये, LM = 3.6 सेमी, ∠L = 50°, LN = 4.2 सेमी आणि `"LM"/"LQ" = 4/7`. तर ΔLQP काढा.
Chapter:
नदीच्या पात्राची रुंदी काढण्यासाठी एका माणसाने पात्राच्या एका काठावरून विरुद्ध काठावर असणाऱ्या मनोऱ्याच्या वरच्या टोकाकडे पाहिले असता 60° मापाचा उन्नत कोन होतो. त्याच रेषेत नदीच्या पात्रापासून 24 मीटर अंतर मागे जाऊन, पुन्हा मनोऱ्याच्या वरच्या टोकाकडे पाहिले असता 30° मापाचा उन्नत कोन होतो, तर नदीपात्राची रुंदी आणि मनोऱ्याची उंची काढा. `(sqrt3 = 1.73)`
Chapter:
गोलाकार बागेचा व्यास 13 मीटर आहे. बागेच्या दोन दरवाजांमधील अंतरही 13 मीटर आहे. बागेच्या परिघावर विजेचा खांब असा उभारायचा आहे की दोन्ही दरवाजांपासून खांबापर्यंत असणाऱ्या अंतरातील फरक 7 मीटर असायला हवा. असा खांब उभारता येईल का? उत्तर होय असल्यास, प्रत्येक दरवाजापासून खांबापर्यंतचे अंतर काढा.
Chapter:
रेषा x − 6y + 11 = 0 ही बिंदू (8, −1) आणि (0, k) जोडणाऱ्या रेखाची दुभाजक आहे, तर k ची किंमत काढा.
Chapter:
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam [इयत्ता १० वी] Mathematics 2 - Geometry [गणित २ - भूमिती] with solutions 2023 - 2024
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam [इयत्ता १० वी] -2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics 2 - Geometry [गणित २ - भूमिती], you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam [इयत्ता १० वी].
How Maharashtra State Board 10th Standard Board Exam [इयत्ता १० वी] Question Paper solutions Help Students ?
• Question paper solutions for Mathematics 2 - Geometry [गणित २ - भूमिती] will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.