Question

ΔABC हा समभूज त्रिकोण आहे. रेख BC वर D बिंदू असा आहे की BD = `1/5` BC, तर `"AD"^2/"AB"^2 = 21/25` हे सिद्‌ध करा.

Answer 1

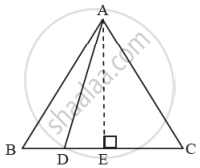
पक्षः ΔABC हा समभूज त्रिकोण आहे.

BD = `1/5` BC

साध्य: `"AD"^2/"AB"^2 = 21/25`

रचना: AE ⊥ BC काढा.

सिद्‌धता:

ΔABC हा समभुज त्रिकोण असल्यामुळे,

∴ AB = BC = AC = x मानू.

ΔABE मध्ये,

∠AEB = 90°   ...(रचना)

∠ABE = 60°   ...(समभुज त्रिकोणाचे कोन)

∴ ∠BAE = 30°   ...(त्रिकोणाचा उर्वरित कोन)

∴ AE = `sqrt3/2` AB   ...(30°-60°-90° प्रमेय)

= `sqrt3/2x`

ΔAED मध्ये, ∠AED = 90°

∴ AD² = AE² + ED²   ...[पायथागोरसचे प्रमेय]

= `(sqrt3/2 x)^2 + ("BE" - "BD")^2`   ... [B-D-E]

पण, BE = `1/2 "BC" = x/2`   ...(समभुज त्रिकोणात शिरोबिंदूपासून काढलेला लंब मध्यगा असते.)

तसेच, BD = `1/5 "BC" = x/5`

∴ AD² = `(3x^2)/4 + (x/2 - x/5)^2`

= `(3x^2)/4 + ((3x)/10)^2`

= `(3x^2)/4 + (9x^2)/100`

= `(84x^2)/100`

= `(21x^2)/25`

∴ AD² = `(21"AB"^2)/25`

∴ `"AD"^2/"AB"^2 = 21/25`