Question

ΔLMN ∼ ΔLQP. ΔLMN मध्ये, LM = 3.6 सेमी, ∠L = 50°, LN = 4.2 सेमी आणि `"LM"/"LQ" = 4/7`. तर ΔLQP काढा.

Answer 1

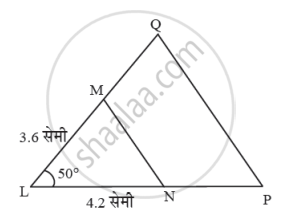
                     कच्ची आकृती

विश्‍लेषण:

आकृतीत दाखवल्याप्रमाणे,

L-N-P आणि L-M-Q मानू.

ΔLMN = ΔLQP   ...(पक्ष)

∴ ∠MLN = ∠QLP   ...(समरूप त्रिकोणांचे संगत कोन)

`"LM"/"LQ" = "MN"/"QP" = "LN"/"LP"`    ...(i) [समरूप त्रिकोणांच्या संगत बाजू]

परंतु, `"LM"/"LQ" = 4/7`   ...(ii) (पक्ष)

∴ `"LM"/"LQ" = "MN"/"QP" = "LN"/"LP" = 4/7`   ...[(i) व (ii) वरून]

∴ ΔLQP च्या बाजू ΔLMN च्या संगत बाजूंपेक्षा मोठ्या आहेत.

∴ जर, रेख LN चे 4 समान भागांत विभाजन केले, तर रेख LP ही रेख LN च्या प्रत्येक समान भागाच्या 7 पट असेल, त्यामुळे जर आपण ΔLMN काढला, तर बिंदू P हा बाजू  LN वर L पासून 7 भाग अंतरावर असेल.

यानंतर, बिंदू P मधून MN ला समांतर रेषा काढल्यास, ती रेषा आणि किरण LM यांचा छेदनबिंदू Q होतो.

ΔLPQ हा अपेक्षित त्रिकोण आहे.

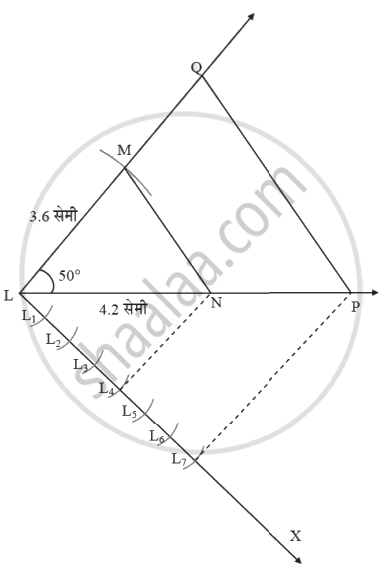
रचनेच्या पायऱ्या:

1. 4.2 सेमी लांबीचा रेख LN काढा.
2. ∠L = 50° घ्या आणि त्यावर 3.6 सेमीचा कंस काढा. बिंदूला M हे नाव द्या.
3. ΔLMN मिळवण्याकरता रेख MN जोडा.
4. किरण LX असा काढा, की ∠NLX हा लघुकोन असेल.
5. किरण LX वर L₁, L₂, L₃, L₄, L₅, L₆, L₇ हे बिंदू असे घ्या, की LL₁ = L₁L₂ = L₂L₃ = L₃L₄ = L₄L₅ = L₅L₆ = L₆L₇.
6. बिंदू N आणि L₄ जोडा.
7. बिंदू L मधून रेख NL₄ ला समांतर रेषा काढा जी रेषा LM ला बिंदू Q मध्ये छेदेल.
8. बिंदू P मधून रेषा MN ला समांतर रेषा काढा जी रेषा LM ला बिंदू Q मध्ये छेदेल. ΔLQP हा ΔLMN शी समरूप असलेला अपेक्षित त्रिकोण आहे.