Advertisements
Advertisements
प्रश्न
Given: In the figure, point A is in the exterior of the circle with centre P. AB is the tangent segment and secant through A intersects the circle in C and D.
To prove: AB2 = AC × AD
Construction: Draw segments BC and BD.
Write the proof by completing the activity.
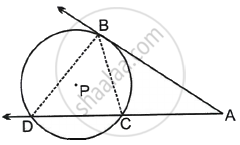
Proof: In ΔABC and ΔADB,
∠BAC ≅ ∠DAB .....becuase ______
∠______ ≅ ∠______ ......[Theorem of tangent secant]
∴ ΔABC ∼ ΔADB .......By ______ test
∴ `square/square = square/square` .....[C.S.S.T.]
∴ AB2 = AC × AD
Proved.
रिकाम्या जागा भरा
बेरीज
उत्तर
Proof: In ΔABC and ΔADB,
∠BAC ≅ ∠DAB .....because common angle
∠ABC ≅ ∠ADB ......[Theorem of tangent secant]
∴ ΔABC ∼ ΔADB .......By AA test
∴ `bb(AB)/bb(AD) = bb(AC)/bb(AB)` .....[C.S.S.T.]
∴ AB2 = AC × AD
Proved.
shaalaa.com
Tangent Secant Segments Theorem
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?