Advertisements
Advertisements
प्रश्न
(i) Construct a triangle ABC, in which AB = 5.0 cm, BC = 3.5 cm and ∠ ABC = `67 1/2°`
( Use a pair of compasses and ruler only.)
(ii) Construct a circle to touch AB at B and it pass though C.
उत्तर
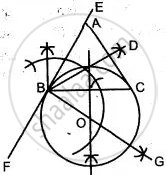
Steps of construction:
1) Draw BC = 3.5 cm.
2) At B draw BE such that ∠ EBC = `67 1/2°`. From BE cut off BA = 5 cm
3) Join AC. Then ΔABC is the required triangle.
4) Produce EB to F.
5) At B draw BG such that ∠ EBG = 90°.
6) Draw perpendicular bisector of BC to cut BG at O.
7) With O as centre and OB as radius draw a circle. This is the required circle to touch AB at B and pass-through C.
APPEARS IN
संबंधित प्रश्न
Using ruler and compasses only,
- Construct triangle ABC, having given BC = 7 cm, AB – AC = 1 cm and ∠ABC = 45°.
- Inscribe a circle in the ΔABC constructed in (i) above. Measure its radius.
Using ruler and compasses only, draw an equilateral triangle of side 5 cm. Draw its inscribed circle. Measure the radius of the circle.
Perpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
- What do you call the point O?
- What is the relation between the distances OA, OB and OC?
- Does the perpendicular bisector of BC pass through O?
Construct Δ ABC in which AB = 5 cm, BC = 4. 5 cm and ∠ ABC = 60" .. Construct a cirde to circumscribe. Δ ABC.
Draw a circle of radius 2. 5 cm and circumscribe a square about it.
Draw line segments OA = 4.5 cm, OB = 3.2 cm such that ∠ AOB = 45°. Construct a circle touching OA at A and passing through B.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB.
Construct a triangle ABC, given that the radius of the circumcircle of triangle ABC is 3.5 cm, ∠ BCA = 45° and ∠ BAC = 60°.
Using ruler and compass only, construct a triangle ABC such that AB = 5 cm, ABC = 75°, and the radius of the circumcircle of triangle ABC is 3.5 cm. On the same diagram, construct a circle, touching AB at its middle point and also touching the side AC.
Use ruler and compasses only for this question:
(i) Construct A ABC, where AB = 3.5 cm, BC = 6 cm and ∠ ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC, and also equidistant from B and C. Measure and record the length of PB.
