Advertisements
Advertisements
प्रश्न
If a, b, c are in continued proportion, prove that: `(pa^2+ qab+ rb^2)/(pb^2+qbc+rc^2) = a/c`
उत्तर
Given a, b, c are in continued proportion
`(pa^2+ qab+ rb^2)/(pb^2+qbc+rc^2) = a/c`
Let `a/b = b/c` = k
⇒ a = bk and b = ck ....(i)
⇒ a = (ck)k = ck2 ...[Using (i)]
and b = ck
L.H.S. = `a/c`
= `(ck^2)/c`
= k2
R.H.S. = `(p(ck^2)^2 + q(ck^2)ck + r(ck)^2)/(p(ck)^2 + q(ck)c + rc^2)`
= `(pc^2k^4 + qc^2k^3 + rc^2k^2)/(pc^2k^2 + qc^2k + rc^2)`
= `(c^2k^2)/(c^2)[(pk^2 + qk + r)/(pk^2 + qk + r)]`
= k2 ...(iii)
From (ii) and (iii), L.H.s. = R.H.S.
∴ b = ck, a = bk = c k k = ck2
(i) L.H.S.
= `"a + b"/"b + c"`
= `(ck^2 + ck)/"ck + c"`
= `(ck(k + 1))/(c(k + 1)`
= k
R.H.S.
= `(a^2(b - c))/(b^2(a - b)`
= `((ck^2)^2(ck - c))/((ck)^2(ck^2 - ck)`
= `(c^2k^4c(k - 1))/(c^2k^2(k - 1)`.
APPEARS IN
संबंधित प्रश्न
Find two numbers such that the mean proportional between them is 12 and the third proportional to them is 96.
Find the fourth proportional to 3, 12, 15
Find the value of x in each of the following proportions:
51 : 85 : : 57 : x
Write (T) for true and (F) for false in case of the following:
51 : 68 : : 85 : 102
The angles of a triangle are in the ratio 3 : 1 : 2. The measure of the largest angle is
If `x/a = y/b = z/c`, prove that `x^3/a^2 + y^3/b^2 + z^3/c^2 = (x+ y+ z)^3/(a + b+ c)^2`
If a, b, c, d are in continued proportion, prove that: (a + d)(b + c) – (a + c)(b + d) = (b – c)2
Sleeping time of a python in a 24 hour clock is represented by the shaded portion in figure.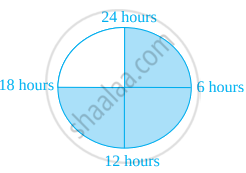
The ratio of sleeping time to awaking time is ______.
What number must be added to each of the numbers 4, 6, 8, 11 in order to get the four numbers in proportion?
The mean proportion between `3 + 2sqrt(2)` and `3 - 2sqrt(2)` is ______.
