Advertisements
Advertisements
प्रश्न
If `vec"a" + vec"b" + vec"c"` = 0, show that `vec"a" xx vec"b" = vec"b" xx vec"c" = vec"c" xx vec"a"`. Interpret the result geometrically?
उत्तर
Given that `vec"a" + vec"b" + vec"c"` = 0
So, `vec"a" xx (vec"a" + vec"b" + vec"c") = vec"a" xx 0`
⇒ `vec"a" xx vec"a" + vec"a" xx vec"b" + vec"a" xx vec"c"` = 0
⇒ `vec"0" + vec"a" xx vec"b" + vec"a" xx vec"c"` = 0 ....`(vec"a" xx vec"a" = 0)`
⇒ `vec"a" xx vec"b" - vec"c" xx vec"a"` = 0 ....`(vec"a" xx vec"c" = -vec"c" xx vec"a")`
⇒ `vec"a" xx vec"b" = vec"c" xx vec"a"` .....(i)
Now `vec"a" + vec"b" + vec"c"` = 0
⇒ `vec"b" xx (vec"a" + vec"b" + vec"c") = vec"b" xx 0`
⇒ `vec"b" xx vec"a" + vec"b" xx vec"b" xx vec"c"` = 0
⇒ `vec"b" xx vec"a" + vec0 + vec"b" xx vec"c"` = 0 ....`(because vec"b" xx vec"b" = 0)`
⇒ `-(vec"a" xx "b") + vec"b" xx vec"c"` = 0
∴ `vec"b" xx vec"c" = vec"a" xx vec"b"` ....(ii)
From equation (i) and (ii) we get
`vec"a" xx vec"b" = vec"b" xx vec"c" = vec"c" xx vec"a"`.
Hence proved.
Geometrical Interpretation
According to figure, we have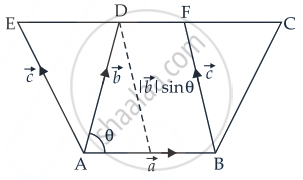
Area of parallelogram ABCD is
⇒ `|vec"a" xx vec"b"| = |vec"a"||vec"b"| sin theta`
Since, the parallelograms on the same base and between the same parallel lines are equal in area
∴ `|vec"a" xx vec"b"| = |vec"b" xx vec"c"| = |vec"c" xx vec"a"|`
⇒ `vec"a" xx vec"b" xx vec"c" = vec"c" xx vec"a"`.
APPEARS IN
संबंधित प्रश्न
If a unit vector `veca` makes angles `pi/3` with `hati,pi/4` with `hatj` and acute angles θ with ` hatk,` then find the value of θ.
Write the value of `vec a .(vecb xxveca)`
If `veca=hati+2hatj-hatk, vecb=2hati+hatj+hatk and vecc=5hati-4hatj+3hatk` then find the value of `(veca+vecb).vec c`
If `veca=2hati+hatj+3hatk and vecb=3hati+5hatj-2hatk` ,then find ` |veca xx vecb|`
Find x such that the four points A(4, 1, 2), B(5, x, 6) , C(5, 1, -1) and D(7, 4, 0) are coplanar.
A line passing through the point A with position vector `veca=4hati+2hatj+2hatk` is parallel to the vector `vecb=2hati+3hatj+6hatk` . Find the length of the perpendicular drawn on this line from a point P with vector `vecr_1=hati+2hatj+3hatk`
if `|vecaxxvecb|^2+|veca.vecb|^2=400 ` and `|vec a| = 5` , then write the value of `|vecb|`
If `vecr=xhati+yhatj+zhatk` ,find `(vecrxxhati).(vecrxxhatj)+xy`
Find `veca.(vecbxxvecc), " if " veca=2hati+hatj+3hatk, vecb=-hati+2hatj+hatk " and " vecc=3hati+hatj+2hatk`
Using vectors find the area of triangle ABC with vertices A(1, 2, 3), B(2, −1, 4) and C(4, 5, −1).
Find the angle between the vectors `vec"a" + vec"b" and vec"a" -vec"b" if vec"a" = 2hat"i"-hat"j"+3hat"k" and vec"b" = 3hat"i" + hat"j"-2hat"k", and"hence find a vector perpendicular to both" vec"a" + vec"b" and vec"a" - vec"b"`.
Find the angle between the vectors `2hat"i" - hat"j" + hat"k"` and `3hat"i" + 4hat"j" - hat"k"`.
Using vectors, find the area of the triangle ABC with vertices A(1, 2, 3), B(2, – 1, 4) and C(4, 5, – 1).
Using vectors, prove that the parallelogram on the same base and between the same parallels are equal in area.
If `vec"a" = hat"i" + hat"j" + hat"k"` and `vec"b" = hat"j" - hat"k"`, find a vector `vec"c"` such that `vec"a" xx vec"c" = vec"b"` and `vec"a"*vec"c"` = 3.
The vectors from origin to the points A and B are `vec"a" = 2hat"i" - 3hat"j" + 2hat"k"` and `vec"b" = 2hat"i" + 3hat"j" + hat"k"`, respectively, then the area of triangle OAB is ______.
The value of the expression `|vec"a" xx vec"b"|^2 + (vec"a".vec"b")^2` is ______.
