Advertisements
Advertisements
प्रश्न
If a hollow sphere of internal and external diameters 4 cm and 8 cm respectively melted into a cone of base diameter 8 cm, then find the height of the cone.
Advertisements
उत्तर
In the given problem, we have a hollow sphere of given dimensions;
Internal diameter of the sphere (d) = 4 cm
External diameter of the sphere (D) = 8 cm
Now, the given sphere is molded into a cone,
Diameter of the base of cone (dc) = 8 cm
Now, the volume of hollow sphere is equal to the volume of the cone.
So, let the height of cone = h cm
Therefore, we get
Volume of cone = the volume of hollow sphere
`(1/3) pi ((d_c)/2)^2 h = (4/3) pi ((D/2)^3 -(d/2)^3)`
`(1/3) pi (8/2)^2 (h) = (4/3) pi ((8/2)^3 -(4/2)^3)`
`(1/3)pi (4)^2 (h) = (4/3) pi (64-8)`
Further, solving for h,
` h = ((4/3) pi (56))/((1/3) pi (16))`
`h = ((4)(56))/((16))`
h = 14 cm
So, height of the cone is 14 cm
APPEARS IN
संबंधित प्रश्न
Find the total surface area of a hemisphere of radius 10 cm. [Use π = 3.14]
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹ 16 per 100 cm2.
`["Assume "pi=22/7]`
A right circular cylinder just encloses a sphere of radius r (see figure). Find
- surface area of the sphere,
- curved surface area of the cylinder,
- ratio of the areas obtained in (i) and (ii).
A certain number of metallic cones, each of radius 2 cm and height 3 cm are melted and recast into a solid sphere of radius 6 cm. Find the number of cones.
The surface area of a solid metallic sphere is 2464 cm2. It is melted and recast into solid right circular cones of radius 3.5 cm and height 7 cm. Calculate:
- the radius of the sphere.
- the number of cones recast. (Take π = `22/7`)
Find the surface area of a sphere of radius 14 cm.
The dome of a building is in the form of a hemisphere. Its radius is 63 dm. Find the cost of painting it at the rate of Rs. 2 per sq. m.
A solid sphere of radius 15 cm is melted and recast into solid right circular cones of radius 2.5 cm and height 8 cm. Calculate the number of cones recast.
Find the radius of a sphere whose surface area is 154 cm2.
Mark the correct alternative in each of the following:
In a sphere the number of faces is
The total surface area of a hemisphere of radius r is
A cylindrical rod whose height is 8 times of its radius is melted and recast into spherical balls of same radius. The number of balls will be
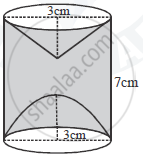
A hemispherical and a conical hole is scooped out of a.solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows:
The height of the solid cylinder is 7 cm, radius of each of hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm.
Give your answer correct to the nearest whole number.Taken`pi = 22/7`.
Find the surface area and volume of sphere of the following radius. (π = 3.14)
4 cm
A sphere has the same curved surface area as the curved surface area of a cone of height 36 cm and base radius 15 cm . Find the radius of the sphere .
A conical tent is to accommodate 77 persons. Each person must have 16 m3 of air to breathe. Given the radius of the tent as 7 m, find the height of the tent and also its curved surface area.
Find the volume and surface area of a sphere of diameter 21 cm.
A spherical cannon ball, 28 cm in diameter is melted and recast into a right circular conical mould, the base of which is 35 cm in diameter. Find the height of the cone, correct to one place of decimal.
The radius of two spheres are in the ratio of 1 : 3. Find the ratio between their volume.
A spherical ball of radius 3 cm is melted and recast into three spherical balls. The radii of two of the balls are 1.5 cm and 2 cm. Find the diameter of the third ball.
