Advertisements
Advertisements
प्रश्न
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height between 65 and 71 inches
उत्तर
Let x denote the height of a student N = 500; m = 68.0 inches and σ = 3.0 inches the standard normal variate
z = `(x - mu)/sigma = (x - 68)/3`
P(Between 65 and 71 inches)
P(65 ≤ x ≤ 71)
When x = 65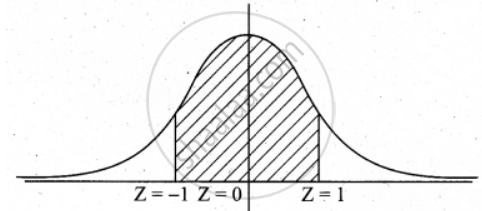
z = `(65 - 68)/3 = (-3)/3 = - 1`
When x = 71
z = `(71 - 68)/3 = 3/3` = 1
P(65 ≤ x ≤ 71) = P(– 1 < z < 1)
= P(– 1 < z < 0) + P(0 < z < 1)
= P(0 < z < 1) + P(0 < z < 1)
= 2 × [P(0 < z < 1)]
= 2 × 0.3413
= 0.6826
∴ Number of students whose height between 65 and 7 inches
= 0.6826 × 500
= 341.3
= 342 .......(approximately)
APPEARS IN
संबंधित प्रश्न
If 18% of the bolts produced by a machine are defective, determine the probability that out of the 4 bolts chosen at random atmost 2 will be defective
An experiment succeeds twice as often as it fails, what is the probability that in next five trials there will be at least three successes
Write the conditions for which the poisson distribution is a limiting case of binomial distribution
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be exactly 3 calls
The distribution of the number of road accidents per day in a city is poisson with mean 4. Find the number of days out of 100 days when there will be at most 3 accidents
Choose the correct alternative:
If X ~ N(9, 81) the standard normal variate Z will be
Choose the correct alternative:
In turning out certain toys in a manufacturing company, the average number of defectives is 1%. The probability that the sample of 100 toys there will be 3 defectives is
Choose the correct alternative:
Which of the following statements is/are true regarding the normal distribution curve?
Choose the correct alternative:
In a binomial distribution, the probability of success is twice as that of failure. Then out of 4 trials, the probability of no success is
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn less than $40,000?
