Advertisements
Advertisements
प्रश्न
In a photographic process, the developing time of prints may be looked upon as a random variable having the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second. Find the probability that it will take less than 16.35 seconds to develop prints
Advertisements
उत्तर
Let x be the random variable have long the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second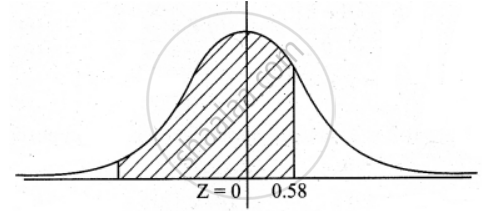
µ = 16,28 and σ = 0.12
The standard normal variate
z = `(x - mu)/sigma = (x - 16.28)/0.12` = 1
P(Less than 16.35 seconds) = P(x < 16.35)
When x = 16.35
z = `(16.35 - 16.28)/0.12 = 0.17/0.12` = 0.583
P(X < 16.35) = P(Z < 0.583)
= P(`-oo` < z < 0) + P(0 < z < 0.583)
= 0.5 + 0.2190
= 0.7190
APPEARS IN
संबंधित प्रश्न
If 5% of the items produced turn out to be defective, then find out the probability that out of 20 items selected at random there are exactly 4 defectives
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers, what is the probability that 3 will have a laptop?
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers, what is the probability that atleast three of the travelers have a laptop?
Mention the properties of poisson distribution
The distribution of the number of road accidents per day in a city is poisson with mean 4. Find the number of days out of 100 days when there will be atleast 2 accidents
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height greater than 72 inches
Choose the correct alternative:
In a parametric distribution the mean is equal to variance is
Choose the correct alternative:
The random variable X is normally distributed with a mean of 70 and a standard deviation of 10. What is the probability that X is between 72 and 84?
The annual salaries of employees in a large company are approximately normally distributed with a mean of $50,000 and a standard deviation of $20,000. What percent of people earn less than $40,000?
People’s monthly electric bills in Chennai are normally distributed with a mean of ₹ 225 and a standard deviation of ₹ 55. Those people spend a lot of time online. In a group of 500 customers, how many would we expect to have a bill that is ₹ 100 or less?
