Advertisements
Advertisements
प्रश्न
If the heights of 500 students are normally distributed with mean 68.0 inches and standard deviation 3.0 inches, how many students have height greater than 72 inches
उत्तर
Let x denote the height of a student N = 500; m = 68.0 inches and σ = 3.0 inches the standard normal variate
z = `(x - mu)/sigma = (x - 68)/3`
P(Greater than 72 inches)
P = P(X > 72)
When x = 72
z = `(72 - 68)/3 = 4/3` = 1.33
P(x > 72) = P(z > 1.33)
= 0.5 – 0.4082
= 0.0918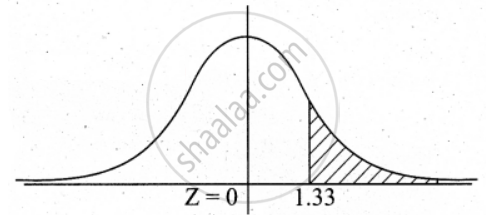
Number of students whose height are greater than 72 inches
= 0.0918 × 500
= 45.9
= 46 ......(approximately)
APPEARS IN
संबंधित प्रश्न
If 5% of the items produced turn out to be defective, then find out the probability that out of 20 items selected at random there are exactly 4 defectives
Out of 750 families with 4 children each, how many families would be expected to have children of both sexes? Assume equal probabilities for boys and girls.
Forty percent of business travellers carry a laptop. In a sample of 15 business travelers, what is the probability that 3 will have a laptop?
An experiment succeeds twice as often as it fails, what is the probability that in next five trials there will be three successes
The average number of phone calls per minute into the switchboard of a company between 10.00 am and 2.30 pm is 2.5. Find the probability that during one particular minute there will be atleast 5 calls
In a photographic process, the developing time of prints may be looked upon as a random variable having the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second. Find the probability that it will take less than 16.35 seconds to develop prints
Choose the correct alternative:
If Z is a standard normal variate, the proportion of items lying between Z = – 0.5 and Z = – 3.0 is
Choose the correct alternative:
Cape town is estimated to have 21% of homes whose owners subscribe to the satellite service, DSTV. If a random sample of your home is taken, what is the probability that all four homes subscribe to DSTV?
If electricity power failures occur according to a Poisson distribution with an average of 3 failures every twenty weeks, calculate the probability that there will not be more than one failure during a particular week
X is a normally distributed variable with mean µ = 30 and standard deviation σ = 4. Find P(X < 40)
