Advertisements
Advertisements
प्रश्न
If X and Y are two sets such that n(X) = 17, n(Y) = 23 and n(X ∪ Y) = 38, find n(X ∩Y).
उत्तर
It is given that:
n(X) = 17, n(Y) = 23, n(X ∪ Y) = 38
n(X ∩ Y) = ?
We know that:
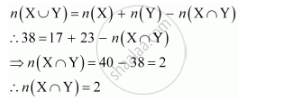
APPEARS IN
संबंधित प्रश्न
If X and Y are two sets such that X ∪Y has 18 elements, X has 8 elements and Y has 15 elements; how many elements does X ∩Y have?
In a group of 400 people, 250 can speak Hindi and 200 can speak English. How many people can speak both Hindi and English?
If S and T Are Two Sets Such that S Has 21 Elements, T Has 32 Elements, and S ∩ T Has 11 Elements, How Many Elements Does S ∪ T Have?
If X and Y are two sets such that X has 40 elements, X ∪Y has 60 elements and X ∩Y has 10 elements, how many elements does Y have?
In a group of 70 people, 37 like coffee, 52 like tea, and each person likes at least one of the two drinks. How many people like both coffee and tea?
In a group of 65 people, 40 like cricket, 10 like both cricket and tennis. How many like tennis only and not cricket? How many like tennis?
In a committee, 50 people speak French, 20 speak Spanish and 10 speak both Spanish and French. How many speak at least one of these two languages?
In a group of students 100 students know Hindi, 50 know English and 25 know both. Each of the students knows either Hindi or English. How many students are there in the group?
In a survey of 60 people, it was found that 25 people read newspaper H, 26 read newspaper T, 26 read newspaper I, 9 read both H and I,11 read both H and T, 8 read both T and I, 3 read all three newspapers. Find:
(i) the number of people who read at least one of the newspapers.
(ii) the number of people who read exactly one newspaper.
For two sets [A \cup B = A\] iff
If A and B are two sets such that \[n \left( A \right) = 70, n \left( B \right) = 60, n \left( A \cup B \right) = 110\] then \[n \left( A \cap B \right)\]
If A and B are two given sets, then \[A \cap \left( A \cap B \right)^c\]
If A = {x : x is a multiple of 3} and , B = {x : x is a multiple of 5}, then A − B is
In a city 20% of the population travels by car, 50% travels by bus and 10% travels by both car and bus. Then, persons travelling by car or bus is
If \[A \cap B - B\]
An investigator interviewed 100 students to determine the performance of three drinks: milk, coffee and tea. The investigator reported that 10 students take all three drinks milk, coffee and tea; 20 students take milk and coffee; 25 students take milk and tea; 12 students take milk only; 5 students take coffee only and 8 students take tea only. Then the number of students who did not take any of three drinks is
For any two sets A and B, \[A \cap \left( A \cup B \right)'\]is equal to
