Question

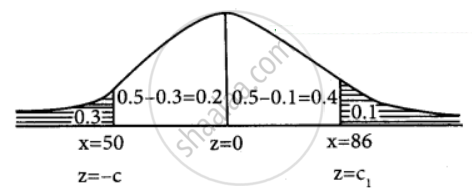
In a distribution 30% of the items are under 50 and 10% are over 86. Find the mean and standard deviation of the distribution

Answer 1

z = `(x - mu)/sigma`

Given that

P(X < 50) = 0.3

P(X > 86) = 0.1

P(X < – c) = 0.3

P(– c < z < 0) = 0.5 – 0.3

P(– c < z < 0) = 0.2  .....{From the table}

P(0 < z < c) = 0.2

c = 0.53

Then – c = – 0.53

∴ `(50 - mu)/sigma` =  – 0.53

50 – µ = -0.53σ

µ – 0.53, σ = 50 → 1

P(X < 50) = 0.1

P(0 < z < ∞) = – P(0 < z < c₁) = 0.1

P(0 < z < ∞) = P(0 < z < c₁) + 0.1

0.5 = P(0 < z < c₁) + 0.1

P(0 < z < c₁) = 0.5 – 0.1

P = (0 < z < c₁) = 0.4

c₁ = 1.29

∴ `(86 - mu)/sigma` = 1.29

86 – µ = 1.29 σ

µ + 1.29σ = 86 → 2

Solving eqn 1 & 2

Equation 2 ⇒ m + 1.2 σ = 86

Equation 1 ⇒ m + 0.53 σ = 50

– + – ………….

………… 1.82 ………… σ = 36 ………….

σ = `36/1.82`

∴ = 19.78

Substitute σ = 19.78 in equation 1

µ – 0.53(19.78) = 50

µ – 10.48 = 50

µ = 50 + 10.48

µ = 60.48

Mean = 60.48 and standard deviation = 19.78