Advertisements
Advertisements
प्रश्न
In a G.P. the product of three consecutive terms is 27 and the sum of the product of two terms taken at a time is `57/2`. Find the three terms
उत्तर
Let the three consecutive terms in a G.P. are `"a"/"r"`, a, ar.
Their Product = `"a"/"r" xx "a" xx "ar"` = 27
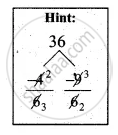
a3 = 27 = 33
a = 3
Sum of the product of terms taken two at a time is `57/2`
`"a"/"r" xx "a" + "a" xx "ar" + "ar" xx "a"/"r" = 57/2`
`"a"^2/"r" + "a"^2"r" + "a"^2 = 57/2`
`3^2(1/"r" + "r" + 1) = 57/2`
`(1 + "r"^2 + "r")/"r" = 57/2 xx 1/9 = 57/18`
18 + 18r2 + 18r = 57r
18r2 + 18r – 57r + 18 = 0
18r2 – 39r + 18 = 0 ÷ 3
⇒ 6r2 – 13r + 6 = 0
`("r" - 2/3)("r" - 3/2)` = 0
r = `2/3, 3/2`
If a = 3, r = `2/3`
∴ The three numbers is `3/(2/3), 3, 3 xx 2/3`
or `3 xx 2/3, 3, 3 xx 2/3`
`9/2, 3, 2`
If a = 3, r = `3/2`, the three numbers is
`"a"/"r", "a", "ar" = 3/(3/2), 3, 3 xx 3/2`
= `6/3, 3, 9/2`
= `2, 3, 9/2`
APPEARS IN
संबंधित प्रश्न
Identify the following sequence is in G.P.?
3, 9, 27, 81, …
Identify the following sequence is in G.P.?
1, −5, 25, −125, ...
Write the first three terms of the G.P. whose first term and the common ratio are given below
a = 6, r = 3
In a G.P. 729, 243, 81, … find t7
Find x so that x + 6, x + 12 and x + 15 are consecutive terms of a Geometric Progression
In a G.P. the 9th term is 32805 and 6th term is 1215. Find the 12th term
Find the 10th term of a G.P. whose 8th term is 768 and the common ratio is 2
For a sequence (tn), if Sn = 5(2n - 1) then tn = ______.
If A, B, C are pth, qth and rth terms of a GP respectively then Aq - r · Br - p · Cp - q = ______.
The sum of the first 10 terms of the series 9 + 99 + 999 + ..., is ______.
