Question

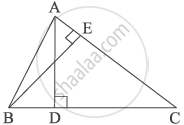
In ΔABC, altitudes AD and BE are drawn. If AD = 7 cm, BE = 9 cm and EC = 12 cm then, find the length of CD.

Answer 1

Given, AD = 7 cm, BE = 9 cm, EC = 12 cm then, CD = ?

Let CD = x cm

In ΔBEC, ∠BEC = 90°      ...(As BE ⊥ AC given)

⇒ from Pythagoras theorem,

`BC = sqrt(BE^2 + EC^2)`

= `sqrt(9^2 + 12^2)`  cm

= `sqrt(81 + 144)` cm

= `sqrt225` cm

BC = 15 cm

⇒ BD = (15 − x) cm

Now Area ΔABC = `1/2 xx BC xx AD`

= `1/2 xx AC xx BE`

{As area of ΔABC = `1/2` base × height}

⇒ `1/2 xx 15 xx 7 = 1/2 AC xx 9`

⇒ AC = `(15 xx 7)/9 = 35/3` cm

Now, ln ΔADC,

∠ADC = 90°

So, Again from Pythagoras theorem,

DC² = AC² − AD²

DC = `sqrt((35/3)^2 - 7^2)` cm

= `7 * sqrt(5^2/3^2 - 1^2)` cm

= `7 * sqrt((25 - 9)/9)` cm

= `7 * 4/3` cm

= `28/3` cm

⇒ DC = `28/3` cm