Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.
उत्तर
Here AB = 5.6 cm, AD = 1.4 cm, BD = AB – AD
= 5.6 – 1.4
= 4.2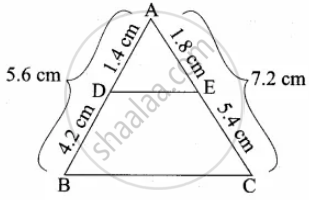
AC = 7.2 cm, AE = 1.8 cm, EC = AC – AE
= 7.2 – 1.8
EC = 5.4 cm
`"AD"/"DB" = 1.4/4.2 = 1/3`
`"AE"/"EC" = 1.8/5.4 = 1/3`
`"AE"/"EC" = "AD"/"DE"`
By converse of basic proportionality theorem DE || BC
APPEARS IN
संबंधित प्रश्न
In ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC
If `"AD"/"DB" = 3/4` and AC = 15 cm find AE
In ΔABC, D and E are points on the sides AB and AC respectively. For the following case show that DE || BC
AB = 12 cm, AD = 8 cm, AE = 12 cm and AC = 18 cm
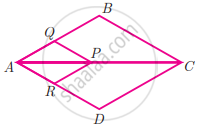
If PQ || BC and PR || CD prove that `"AR"/"AD" = "AQ"/"AB"`
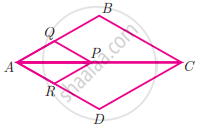
If PQ || BC and PR || CD prove that `"QB"/"AQ" = "DR"/"AR"`
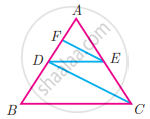
In trapezium ABCD, AB || DC, E and F are points on non-parallel sides AD and BC respectively, such that EF || AB. Show that = `"AE"/"ED" = "BF"/"FC"`
DE || BC and CD || EE Prove that AD2 = AB × AF
Construct a ∆PQR in which the base PQ = 4.5 cm, ∠R = 35° and the median from R to RG is 6 cm.
Construct a ∆ABC such that AB = 5.5 cm, ∠C = 25° and the altitude from C to AB is 4 cm
ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is
Two circles intersect at A and B. From a point, P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
