Question

In ΔABC if sin²A + sin²B = sin²C and l(AB) = 10, then the maximum value of the area of ΔABC is ______ 

पर्याय

• 50

• `10sqrt2`

• 25

• `25sqrt2`

Answer 1

In ΔABC if sin²A + sin²B = sin²C and l(AB) = 10, then the maximum value of the area of ΔABC is 25.

Explanation:

 

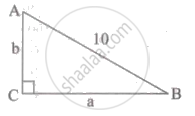
sin²A + sin²B = sin²C

⇒ sin C = 1 ⇒ C = `pi/2`

`a/sinA = b/sinB = c/sinC`

⇒ `a/sinA = b/sinB = 10/1`

⇒ a = 10 sin A, b = 10 sin B

A(ΔABC) = `1/2ab = 1/2(10 sinA)(10 sinB)`

= `1/2 xx 100 xx sinA xx sinB`

Maximum value of sin A sin B = `1/2`

∴ A(ΔABC) = `1/2 xx 100 xx 1/2`

= 25 sq. units.