Advertisements
Advertisements
प्रश्न
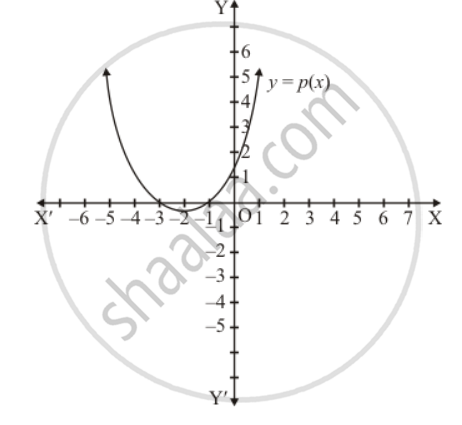
In Fig. 2.17, the graph of a polynomial p(x) is given. Find the zeros of the polynomial.
उत्तर
Just see the point of intersection of the curve and x-axis and find out the x-coordinate of these points. These x-coordinates will be the zeros of the polynomial Since the intersection points are
`(-3,0)` and `(-1,0)`
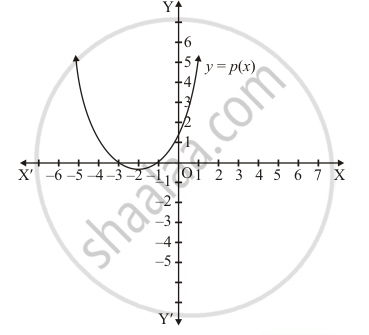
Hence, the zeros of the polynomial is -3 and -1
APPEARS IN
संबंधित प्रश्न
If α, β are the zeros of a polynomial such that α + β = −6 and αβ = −4, then write the polynomial.
If one zero of the polynomial f(x) = (k2 + 4)x2 + 13x + 4k is reciprocal of the other, then k=
If f(x) = ax2 + bx + c has no real zeros and a + b + c = 0, then
State whether the given algebraic expression is polynomial. Justify.
`2m^(-2) + 7m - 5`
Identify the following expression is polynomial. If not give reason:
`1/(x^(-2)) + 1/(x^(-1)) + 7`
Given that two of the zeroes of the cubic poly-nomial ax3 + bx2 + cx + d are 0, the third zero is ______.
The number of polynomials having zeroes as 4 and 7 is ______.
Case Study -1

The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that h(t) = -16t2 + 8t + k.
What is the value of k?
Case Study -1

The figure given alongside shows the path of a diver, when she takes a jump from the diving board. Clearly it is a parabola.
Annie was standing on a diving board, 48 feet above the water level. She took a dive into the pool. Her height (in feet) above the water level at any time‘t’ in seconds is given by the polynomial h(t) such that h(t) = -16t2 + 8t + k.
At what time will she touch the water in the pool?
Classify the following as a constant, linear, quadratic and cubic polynomials:
2 – x2 + x3
