Advertisements
Advertisements
प्रश्न
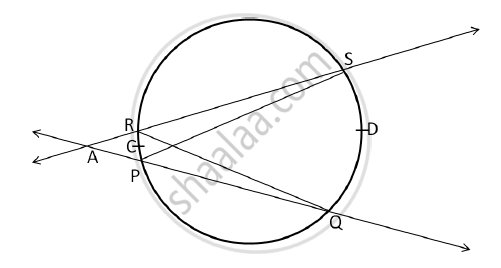
In the following figure, secants containing chords RS and PQ of a circle intersects each other in point A in the exterior of a circle if m(arc PCR) = 26°, m(arc QDS) = 48°, then find:
(i) m∠PQR
(ii) m∠SPQ
(iii) m∠RAQ
उत्तर
Given: m(arc PCR) = 26°, m(arc QDS) = 48°
By Inscribed Angle Theorem,we get
(i) ∠PQR = 1/2 m(arc PCR)
∠PQR = 1/2 x 26º
∠PQR = ∠AQR = 13º ...(1)
(ii) ∠SPQ = 1/2m(arc QDS)
∠SPQ = 1/2 x 48º
∠SPQ = 24º ...(2)
(iii) In ΔAQR, by the Remote Interior Angle theorem,
∠RAQ + ∠AQR = ∠SRQ
∠SRQ = ∠SPQ ...(Angles subtended by the same arc)
i.e. ∠RAQ + ∠AQR = ∠SPQ
m ∠RAQ = m ∠SPQ - m∠AQR
m ∠RAQ = 24º - 13º ...[From (1) and (2)]
m ∠RAQ = 11º
APPEARS IN
संबंधित प्रश्न
In the following figure, m(arc PMQ) = 130o, find ∠PQS.

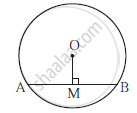
In the adjoining figure, point O is the centre of the cirlcle, seg OM ⊥ chord AB. If OM = 8cm, AB = 12 cm, then find OB.
If the length of an arc of the sector of a circle is 20 cm and if the radius is 7 cm, find the area of the sector.
