Advertisements
Advertisements
प्रश्न
In the following figure, m(arc PMQ) = 130o, find ∠PQS.

उत्तर

Given : m(arc PMQ) = 130°
According to Tangent Chord Theorem,
The tangent chord angle theorem states that the measure of the angle formed by the intersection of a tangent and a chord of the circle equals one half of the intercepted arc by the chord.
∴ ∠PQS = `1/2` m(arc PMQ)
⇒ ∠PQS = `[130°]/2` = 65°
APPEARS IN
संबंधित प्रश्न
In the following figure, secants containing chords RS and PQ of a circle intersects each other in point A in the exterior of a circle if m(arc PCR) = 26°, m(arc QDS) = 48°, then find:
(i) m∠PQR
(ii) m∠SPQ
(iii) m∠RAQ
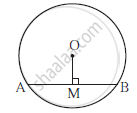
In the adjoining figure, point O is the centre of the cirlcle, seg OM ⊥ chord AB. If OM = 8cm, AB = 12 cm, then find OB.
If the length of an arc of the sector of a circle is 20 cm and if the radius is 7 cm, find the area of the sector.
