Advertisements
Advertisements
प्रश्न
In given figure, two tangents PT and QT are drawn to a circle with centre O from an external point T. Prove that `angle`PTQ = 2`angle`OPQ.
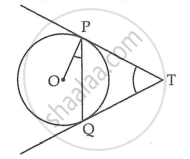
उत्तर
Given that,
TP and TQ are tangents to circle
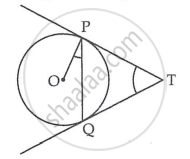
To prove: `angle`PTQ = 2`angle`OPQ
We have,
TP = TQ ...[Lengths of tangents from an external point to a circle are equal]
`angle`TQP = `angle`TPQ ...(i) [angles of equal sides are equal]
Also, `angle`OPT = 90° ...[Radius is perpendicular to tangent at point of contact]
⇒ `angle`OPQ + `angle`QPT = 90°
⇒ `angle`TPQ = 90° − `angle`OPQ ...(ii)
In `triangle`PTQ, we have,
`angle`PTQ + `angle`TQP + `angle`TPQ = 180° ...[Sum of angles of triangle]
From (i) and (ii),
⇒ `angle`PTQ + `angle`TPQ + `angle`TPQ = 180°
⇒ `angle`PTQ + 2( 90° − `angle`OPQ) = 180°
⇒ `angle`PTQ + 180° − 2`angle`OPQ = 180°
⇒ `angle`PTQ = 2`angle`OPQ
Hence, proved.
